Coördinatenstelsels in het platte vlak

Overzicht  ][  Meetkunde | Anal.Meetkunde

---

Zie ook de pagina "Meer over barycentrische coördinaten"

Overzicht

1. Hoekcoördinaten
2. Tripolaire coördinaten
3. Barycentrische coördinaten
4. Normaalcoördinaten (trilineaire coördinaten)
       -  Toegevoegde punten
       -  Verband tussen barycentrische en normaalcoördinaten
       -  Rechte lijnen
5. Referenties

6. Download

---

Naast het gebruikelijke orthogonale (Carthesische) coördinatenstelsel waarmee de plaats van een punt in het platte vlak wordt vastgelegd door de afstand van dat punt tot twee (loodrecht op elkaar staande) snijdende lijnen, zijn er meer manieren om dat te doen.
We gaan daarbij telkens uit van een vaste driehoek ABC (de basisdriehoek of referentiedriehoek) en een punt P in het vlak van die driehoek.
We maken verder de volgende afspraak:
Met S(XYZ) wordt bedoeld de oppervlakte van de driehoek XYZ.

1. Hoekcoördinaten

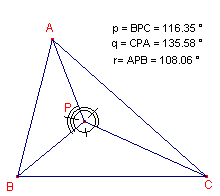
Definitie De grootte van de hoeken BPC, CPA en APB zijn, in deze volgorde, de hoekcoördinaten (ook wel angulaire coördinaten) van het punt P tov. driehoek ABC. AB, BC en CA heten de referentiezijden van deze coördinaten. De coördinaten kunnen worden uitgedrukt in graden of radialen.

Tekenafspraak
Het teken van zo’n coördinaat is positief als P en het hoekpunt tegenover de referentiezijde aan dezelfde kant van de referentiezijde liggen. Is dit niet het geval, dan is de coördinaat negatief.

Stelling 1 De hoekcoördinaten (p, q, r), in radialen, van een punt P tov. een driehoek ABC voldoen aan p + q + r º 0 (mod 2p ). of ook Als P binnen de driehoek ligt, dan is p + q + r = 2p ; ligt P buiten de driehoek, dan is p + q + r = 0.

Bewijs:

Als P binnen de driehoek ligt vormen de hoeken een volle hoek (360°).
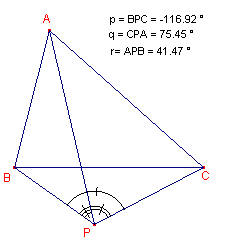
Ligt P buiten de driehoek, dan vormen (in het algemeen) twee van de hoeken samen de derde, die dan negatief wordt gerekend. ¨

Constructie

Uit de definitie blijkt, dat elk drietal coördinaten (p, q, r) éénduidig een punt P in het vlak bepaalt.
Voor de eerste coördinaat geldt dat P op de cirkel ligt met koorde BC waarbij BPC = p.
De tweede coördinaat bepaalt, via de hoek CPA, eenzelfde type cirkel op de koorde CA. Beide cirkels snijden elkaar behalve in C ook in P.
Uit Stelling 1 volgt dan dat ook de derde cirkel (die op de koorde AB) door het punt P gaat.
De plaats van een punt wordt dus door twee getallen, die kunnen dienen als hoekcoordinaten, vastgelegd. ¨

Klik hier voor een CabriJavapplet bij deze paragraaf.

2. Tripolaire coördinaten

Definitie De afstand AP, BP, CP van een punt tot de toppen van een driehoek ABC (de referfentiedriehoek) heten tripolaire afstanden. Elke drie getallen p, q, r met p : q : r = PA : PB : PC worden tripolaire coördinaten van P (tov. ABC) genoemd.

Opmerking
Tripolaire coördinaten hebben geen teken.
[einde Opmerking]

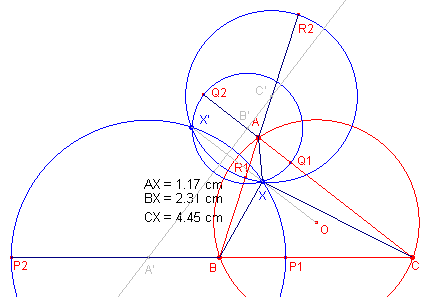Constructie Bij gegeven (p, q, r) zijn P1en P2 de punten die het lijnstuk BC (in en uitwendig) verdelen in de verhouding q/r. De punten P1 en P2 zijn de snijpunten van de lijn BC met de Apollonius-cirkel op BC bij de verhouding q : r. Op dezelfde manier kunnen we punten Q1 en Q2 op CA met verhouding r /p (en eventueel R1 en R2 op AB met verhouding p/q) vinden. Deze cirkels snijden elkaar in de punten X en X'. ¨

Gevolg
Er zijn twee punten die bedoelde tripolaire coördinaten hebben.
De drie cirkels hebben de koorde XX' gemeenschappelijk.
De punten B,C,P1,P2 vormen een harmonisch viertal, waaruit volgt, dat deze Apollonius-cirkels de omcirkel van ABC loodrecht snijden.
Het middelpunt O ligt dus op de lijn XX', waarbij OX× OX' = R² (R is dan de straal van de omcirkel).
De punten X en X' zijn dus elkaars beeld bij inversie tov. de omcirkel.
Ook is nu duidelijk, dat de middelpunten van de Apollonius-cirkels collineair zijn.

Opmerking
Omdat bij gegeven tripolaire coördinaten telkens twee punten X en X' bestaan met die coördinaten, is het werken met dit type coördinaten minder geschikt.
[einde Opmerking]

3. Barycentrische coördinaten

Zie ook de pagina "Meer over barycentrische coördinaten"

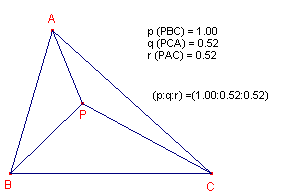
Definitie De verhoudingen tussen de oppervlaktes van de driehoeken PBC, PCA, PAB worden de barycentrische coördinaten van P tov. de referentiedriehoek ABC genoemd.

Opmerking
Meestal wordt één van de coördinaten genormaliseerd op 1.
[einde Opmerking]

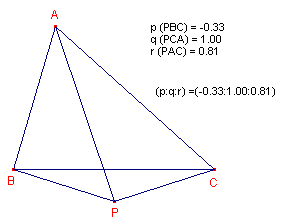Tekenafspraak
Het teken van zo’n coördinaat is positief als P en het hoekpunt tegenover de referentiezijde aan dezelfde kant van de referentiezijde liggen. Is dit niet het geval, dan is de coördinaat negatief (of gelijk aan nul).

Klik hier voor een CabriJavapplet bij deze paragraaf.

Voorbeelden

[1]
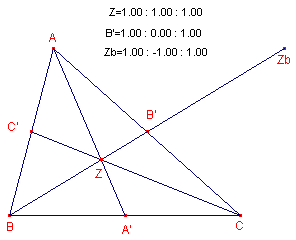
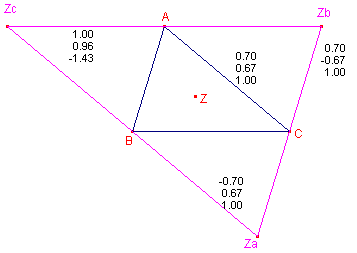
We bekijken de hoekpunten A', B', C' van de centrumdriehoek van de referentiedriehoek ABC. Het zwaartepunt Z van de referentiedriehoek heeft de coördinaten (1 : 1 : 1), immers de oppervlaktes van de drie deeldriehoeken zijn voor het punt Z gelijk.
Z_b is het spiegelbeeld van B = (0 : 1 : 0) in het punt B', waardoor Zb = (1 : -1 : 1).

In dit geval geldt ook:
S(ABC) = S(ZBC) + S(ZCA) + S(ZAB)
zodat
1A + 1B + 1C = 3Z

[2]
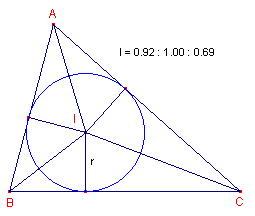
Voor het incentrum I (het middelpunt van de incirkel) van de referentiedriehoek ABC hebben we:
S(IBC) = ½ ra, S(ICA) = ½ rb, S(IAB) = ½ rc
Zodat
I_bary = a : b : c
Verder geldt: S(ABC) = S(IBC) + S(ICA) + S(IAB) = ½ r(a + b + c) = rs
Zodat aA + bB + cC = 2(½ raA + ½ rbB + ½ rcC) = 2I
[einde Voorbeeld]

¤ Zie verder de pagina "Meer over barycentrische coördinaten"

4. Normaalcoördinaten (trilineaire coördinaten)

Definitie Onder de absolute normaalcoördinaten (p, q, r) van een punt P tov. een referentiedriehoek ABC verstaan we de afstanden p, q, r van P tot de zijden BC, CA, AB van de driehoek (in deze volgorde). Onder de (relatieve) normaalcoördinaten of (homogene) normaalcoördinaten van een punt P verstaan we elk drietal p', q', r' dat evenredig is met de absolute normaalcoördinaten van P.

Notatie:

absolute normaalcoördinaten: P(p, q, r)
normaalcoördinaten: P = p : q : r, of ook wel P(p : q : r).
Bij de absolute normaalcoördinaten wordt soms een index r (van reëel) geplaatst om ze te kunnen onderscheiden van de relatieve coördinaten.
Meestal wordt een van de normaalcoördinaten genormaliseerd op 1.
Normaalcoördinaten worden ook wel trilineaire coördinaten of driehoekscoördinaten genoemd.

Tekenafspraak

Het teken van zo’n coördinaat is positief als P en het hoekpunt tegenover de referentiezijde aan dezelfde kant van de referentiezijde liggen. Is dit niet het geval, dan is de coördinaat negatief (of gelijk aan nul).

Klik hier voor een CabriJavapplet bij deze paragraaf.

Stelling 2 Voor de absolute normaalcoordinaten van P(p, q, r) en de zijden a, b, c van de referentiedriehoek geldt: ap + bq + cr = 2S waarbij S de oppervlakte is van de referentiedriehoek.

Gevolg
Bij gegeven p en q (en een gegeven basisdriehoek) ligt de waarde van r vast.
Hierdoor wordt een punt in het vlak vastgelegd door twee getallen die opgevat kunnen worden als absolute normaalcoordinaten van dat punt.

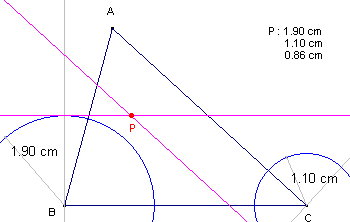Constructie Zijn p > 0 en q > 0 gegeven, dan ligt het punt P op de lijn evenwijdig met BC op (positieve) afstand p van BC. P ligt dan ook op de lijn evenwijdig met CA en op (positieve) afstand q van CA. P is dus het snijpunt van beide lijnen. ¨

Stelling 3 De plaats van een punt P wordt eenduidig vastgelegd door drie homogene normaalcoordinaten.

Bewijs:

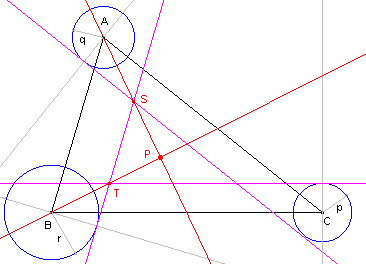Zij P = p : q : r met p, q, r >0. Het punt P is element van de verzameling van de punten X waarvoor de afstanden tot CA en AB zich verhouden als q : r. Deze verzameling is een rechte lijn, welke bepaald wordt door het punt A en het punt S met d(S,CA) = q en d(S, AB) = r. Het punt P ligt op de verzameling van de punten X waarvoor de afstanden tot AB en BC zich verhouden als r : p. Deze verzameling is een rechte lijn die door B gaat en het punt T met d(T, AB)= r en d(T, BC) = p. Het punt P is dan het snijpunt van de lijnen AS en BT. ¨

Toegevoegde punten

Bij elk punt P(p:q:r) kunnen we de punten P_a(–p:q:r), P_b(p:–q:r), P_c(p:q:–r) vinden. Deze worden de toegevoegde punten van P genoemd.

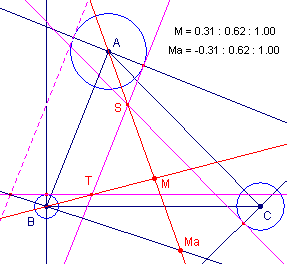Constructie We gaan uit van een gegeven punt M(x : y : z) en construeren het bijbehorende toegevoegde punt Ma(-x : y : z). Nu geldt ondermeer: d(Ma,AB) / z = d(Ma,CA) / y Hieruit volgt dat Ma op de lijn AM ligt. En ook hebben we: d(Ma,BC) / x = d(Ma,AB) / z. Hieruit volgt dat Ma ligt op een lijn door B, waarvan de punten dezelfde verhouding tot BC en AB hebben als de punten op BM, maar dan met tegengesteld teken. Deze lijn heet de ook wel harmonische rechte van MC tov. driehoek ABC. Op dezelfde manier volgt uit d(Ma,CA) / y = d(Ma,BC) / x, dat Ma op een lijn door C ligt, de harmonisch toegevoegde lijn aan CM. ¨

Stelsel toegevoegde punten

Een punt en de drie daaraan toegevoegde punten wordt wel een stelsel toegevoegde punten bij de referentiedriehoek genoemd.
Zo'n stelsel is commutatief: elk punt van het stelsel heeft de andere drie punten als toegevoegde punten.

Voorbeelden

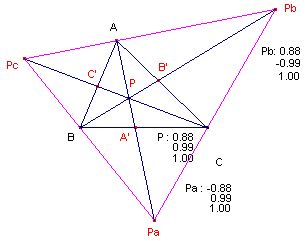	[1] Een drietal in een punt P concurrente cevianen van een driehoek en de vierde harmonische bij het hoekpunt, het punt P en het snijpunt van de ceviaan met de overstaande zijde.
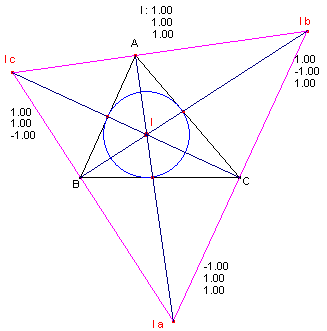	[2] Het middelpunt van de incirkel en de middelpunten van de aancirkels van een driehoek.
	[3] Het zwaartepunt en de hoekpunten van de anticentrumdriehoek (de anticentrumdriehoek A van een driehoek D is de driehoek waarvan driehoek D centrumdriehoek is (de zijden van driehoek A gaan door de toppen van driehoek D en zijn evenwijdig met de daarbij behorende overstaande zijde).

[einde Voorbeelden]

Verband tussen barycentrische en normaalcoördinaten

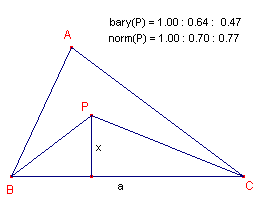
Zij x_r de lengte van het loodlijnstuk uit P op BC. Dan is S(PBC) = ½ax_r.
Voor de eerste barycentrische coördinaat van P hebben we dan: X_bary(P) = ½ax_r ……(1)
Voor de eerste normaalcoördinaat van P geldt: x_norm(P) = x = kx_r ……(2)
We vinden uit (1) en (2):
X_bary : Y_bary : Y_bary = ax : by : cz = ax_norm : by_norm : cz_norm

Omgekeerd:
x_norm : y_norm : z_norm = X_bary / a : Y_bary / b : Z_bary / c

Voorbeelden

[1]
Z is het zwaartepunt van de referentiedriehoek ABC.
Z_bary = 1 : 1 : 1, zodat ax : by : cz = 1 : 1 : 1, waaruit ax = k; by = k; cz = k.
Dit geeft:
x = k/a = kbc/abc; y = k/b = kca/abc; z = k/c = kab/abc
Of:
x : y : z = bc : ca : ab
Met andere woorden: Z_norm = bc : ca : ab

[2]
Voor het incentrum van een driehoek geldt, dat de afstanden tot de zijden gelijk zijn, dus:
I_norm = 1 : 1 : 1, zodat
I_bary = a : b : c

[einde Voorbeelden]

¤ Zie ook de pagina "Meer over barycentrische coördinaten"

Rechte lijnen
Zijn P₁ en P₂ punten met afstanden x_r1 en x_r2 tot BC.
P is een punt van de lijn P₁P₂ waarbij P₁P : PP₂ = l .
Voor de afstand x_r van P tot BC vinden we dan:
   
Of algemeen voor P:
   
Dit is de "parameter-voorstelling" van de lijn P₁P₂.
Eliminatie van l hieruit geeft
   
Deze uitdrukking kunnen we ook schrijven in determinant-vorm:
   
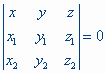
Omkeerd, de vergelijking ux + vy + wz = 0 is een rechte lijn door de punten v : -u : 0, w : 0 : -u en 0 : w : -v.

Oneigenlijke rechte

Voor ieder punt P = x : y : z, met x = kx_r, etc., hebben we: ax_r + by_r + cz_r = 2S.
Hieruit volgt
   
tenzij ax + by + cz = 0
Punten P die hieraan voldoen, liggen op de "lijn" met vergelijking ax + by + cz = 0. Deze lijn noemen we de oneigenlijke rechte.

5. Referenties

[1]		O. BOTTEMA: Hoofdstukken uit de Elementaire Meetkunde, Epsilon (Utrecht, 1997)
[2]		CLARK KIMBERLING: Triangle Centers and Central Triangles, Utilitas Mathematical Publishing Inc. (Winnipeg, Canada, 1998)
[3]		CLARK KIMBERLING: Encyclopedia of Triangle Centers - ETC (website).
[4]		TRAJAN LALESCO: La Géométrie du Triangle, Librairie Vuibart (Parijs, 1952)
[5]		PAUL YIU: The uses of homogeneous barycentric coordinates in plane euclidean geometry, in: International Journal of Mathematical Education in Science and Technology, 31 (2000) 569-578

¤ Zie ook de pagina "Meer over barycentrische coördinaten"

---

6. Download
De in de CabriJavapplets gebruikte figuren kunnen in éen bestand via deze website worden gedownload.
Klik hier om het downloaden te starten (ZIP-bestand; ca. 4kB).

---

[coordsyst.htm] laatste wijziging op: 01-jul-03