Kegelsnede en rechte lijn
Overzicht ][ ProjMeetkunde | CabriMacro's | Meetkunde
- Snijpunten van een kegelsnede en een rechte lijn
- Macro 1
- Tweede snijpunt van een lijn en een kegelsnede
- Macro 2
- Constructie mbv. de Stelling van Pascal (tweede snijpunt met lijn)
1. Snijpunten van een kegelsnede en
een rechte lijn 
| figuur 1 |  |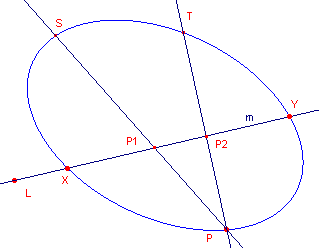
Zij K een kegelsnede. Zij m een lijn die de kegelsnede snijdt. S en T zijn twee vaste punten op K. P is een variabel punt op K. De lijnen PS en PT induceren nu een projectieve afbeelding van m op zichzelf. De snijpunten X en Y van de lijn en de kegelsnede zijn de dekpunten van deze afbeelding. Klik hier |
Een projectiviteit op een lijn wordt vastgelegd door 3 punten en hun beeldpunten.
Voor het vinden van de snijpunten gaan we daarom uit van twee lijnenbundels {S} en {T} en
3 punten A, B, C van de kegelsnede.
| figuur 2 |  |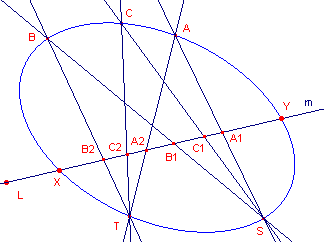
De lijnen S{A,B,C} en T{A,B,C} bepalen nu een projectieve afbeelding van
de punten op de lijn m. De puntenparen zijn (A1, A2), (B1, B2) en (C1, C2). Ook nu zijn de punten X en Y de dekpunten. |
2. Macro 1 - macro:ProjectLijn3P-2D
We beschrijven vervolgens de Cabri-macro:ProjectLijn3P-2D waarmee
we de dekpunten op een lijn m, bij een gegeven drietal punten en hun beeldpunten,
kunnen construeren (zie ook Opmerkingen).
| Constructie: | ||
| figuur 3 |  |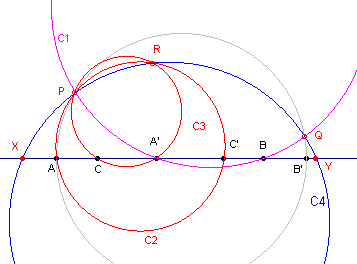
Bij gegeven punten A en A' is m de lijn door deze punten. B, B'
en C, C' kunnen dan op m (met PuntOpObject) worden gekozen. 1 - Cirkel(middellijn AB') 2 - PuntOpObject(1) = P 3 - Omcirkel3P(P, A', B) = C1 Omcirkel3P is een standaard Cabri-macro voor de omgeschreven cirkel van een driehoek. 4 - Snijpunt(1, 3) = Q 5 - Omcirkel3P(P, A, C') = C2 6 - Omcirkel3P(P, A', C) = C3 7 - Snijpunt(C1, C2) = R 8 - Omcirkel3P(P, Q, R) = C4 |
De beginobjecten van de macro zijn (in deze volgorde): de punten A,
A', B, B', C, C'.
Het eindobject is: C4 (dus niet de snijpunten van de cirkel en
de lijn).
N.B.
Na uitvoering van de macro moeten de dubbelpunten (X, Y) worden geconstrueerd als
snijpunten van de lijn en de cirkel (C4).
Klik hier 
voor een CabriJavapplet
van bovenstaande constructie.
Opmerkingen
[1]
Bovenstaande constructie behoort niet tot de projectieve meetkunde. Het begrip
'cirkel' heeft in de projectieve meetkunde geen betekenis: de soort is 'kegelsnede'.
Klik hier voor een CabriJavapplet
waarin bovenstaande macro is toegepast.
[2]
Er is geen direct zichtbaar verschil tussen de manier waarop Cabri zelf de snijpunten van
een lijn en een kegelsnede bepaalt en de manier waarop dit gebeurt met bovenstaande
macro.
3. Tweede snijpunt van een lijn en
een kegelsnede
| figuur 4 |  |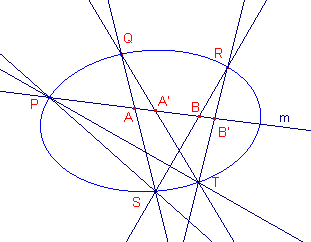
Als de lijn m en de kegelsnede een punt gemeenschappelijk
hebben, dan wordt door de bundels {S} en {T}wederom een projectieve afbeelding van m
opzichzelf geïnduceerd. In dit geval is die afbeelding vastgelegd door de paren (A, A'), (B, B') en (P, P), waarbij P het gemeenschappelijk punt is. Het tweede dekpunt van die projectiviteit is dan het tweede snijpunt van de lijn en de kegelsnede. Zie ook Paragraaf 5 voor een tweede methode. |
4. Macro 2 -
macro:ProjectLijn2P1D-1D
De macro-constructie voor het tweede dekpunt verloopt nu eenvoudiger. In onderstaande
constructiebeschrijving is X het gegeven dekpunt.
In de naamgeving van de macro staat ook nu de P voor Paar en de D
voor Dekpunt.
| figuur 5 |  |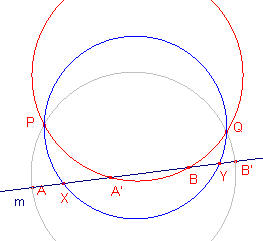
1. Cirkel(middellijn AB') = C1 2. PuntOpObject(1) = P 3. Omcirkel3P(P, A', B) = C2 Omcirkel3P is een standaard Cabri-macro voor de omgeschreven cirkel van een driehoek. 4. Snijpunt(C1 , C2) = Q 5. Omcirkel3P(P, Q, X) = C3 De beginobjecten van de macro zijn: A, A',
B, B', X (in deze volgorde). N.B. |
5. Constructie mbv. de Stelling van
Pascal (tweede snijpunt met lijn)
Op basis van de Stelling van Pascal is
het eveneens mogelijk het tweede snijpunt van een lijn met een kegelsnede te construeren.
| figuur 5 |  |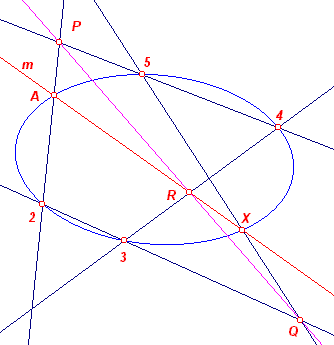
De kegelsnede wordt bepaald door de punten A (het eerste snijpunt van de
lijn m met de kegelsnede) en vier andere punten (in de figuur aangegeven met 2,
3, 4, 5). Zij X het tweede snijpunt van m met de kegelsnede. Volgens de Stelling van Pascal zijn de snijpunten van de overstaande zijden
van de zeshoek A2345X dan collineair. Op basis van deze constructie is de macro:TweedeSnijpuntLijnKegelsnede vastgelegd. |
6. Download
Klik hier om het bestand te downloaden
waarin (bijna) alle op deze pagina staande figuren, en de genoemde macro's zijn opgenomen
(ZIP-bestand, ca. 9kB).
[pkegel.htm] laatste wijziging op: 27-12-04