Raaklijnendriehoek

Overzicht  ][  Bijzondere punten | Meetkunde

Overzicht terug

  1. Inleiding
  2. Raaklijnendriehoek
  3. En meer...
  1. Referenties

1. Inleiding terug
We bewijzen allereerst:

Stelling 1
[1] Het verbindingslijnstuk van het omcentrum met een hoekpunt van een driehoek staat loodrecht op de 'overeenkomstige' zijde van de voetpuntsdriehoek (hoogtepuntsdriehoek) van die driehoek.
[2] Een hoekpunt van een driehoek is het midden van de boog tussen de snijpunten van de hoogtelijnen uit de beide andere hoekpunten met de omcirkel.

Bewijs:

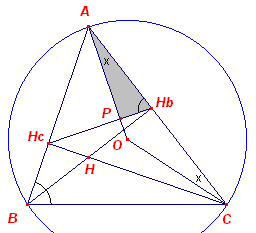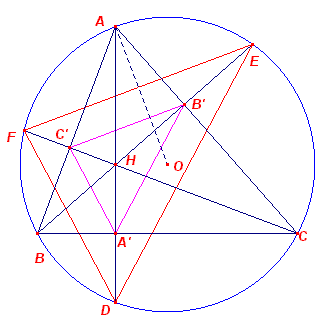
gob1 Bewijs van Stelling 1.1:
In de figuur hiernaast zijn BHb en CHc hoogtelijnen van ABC. HbHc is dus een zijde van de hoogtepuntsdriehoek van ABC. O is het omcentrum van ABC.
We bewijzen dat OA _|_ HbHc.

In OCA is O = 2B, en ook 2A = 2x = 180 - O = 180 - 2B. Waaruit direct volgt: A = 90 - B.
In APHb is Hb = B.
De hoek bij P is dus recht. ¨

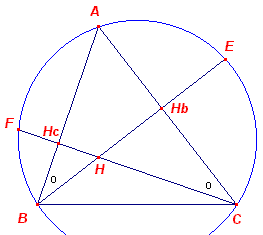gob1b Bewijs van Stelling 1.2:
We dienen dus (o.a.)aan te tonen, dat bg(AE) = bg(AF).
In de figuur hiernaast zijn BHb en CHc weer hoogtelijnen van ABC.

ABHb en ACHc hebben de hoek A en een rechte hoek gemeenschappelijk. De derde hoek is dus ook gelijk.
Daaruit volgt direct dat bg(AE) = bg(AF), omtrekshoeken. ¨

2. Raaklijnendriehoek terug

Definitie
De raaklijnendriehoek (Eng. tangential triangle) van een driehoek is de driehoek gevormd door de raaklijnen in de hoekpunten aan de omcirkel van die driehoek.

Uit Stelling 1.1 volgt nu direct:

Stelling 2
De hoogtepuntsdriehoek en de raaklijnendriehoek van een driehoek zijn gelijkstandig (homothetisch).

Bewijs:

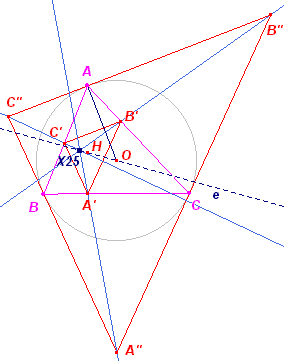gob2 Hiernaast is A'B'C' de voetpuntsdriehoek van ABC en A"B"C" de raaklijnendriehoek.

Nu is:
OA _|_ raaklijn in A aan de omcirkel, maw. OA _|_ B"C"
en
OA _|_B'C' (Stelling 1)
waaruit volgt dat B'C' // B"C", enz.

Er is dus sprake van gelijkstandigheid van A'B'C' en A"B"C". ¨

Opmerkingen
[1]
De omcirkel van ABC is dus de incirkel van A"B"C" (middelpunt O).
Het punt O is dus het incentrum van driehoek A"B"C".
[2]
Het homothetieentrum is het punt dat in de codering van Kimberling wordt aangeduid met X25.
Dit punt wordt incidenteel ook wel het Gob-punt van driehoek ABC genoemd (naar Antoine Gob, 18...-..., België).

[3]
H en O zijn isogonale punten tov. driehoek ABC.
Uit de stelling
Zijn P en Q isognale geconjugeerde punten tov driehoek ABC, dan is de voetpuntsdriehoek van P homothetisch (gelijkstandig) met de antivoetpuntsdriehoek van Q (zie de pagina "Meer over de isogonale verwantschap")
volgt Stelling 2 direct.
[einde Opmerking]

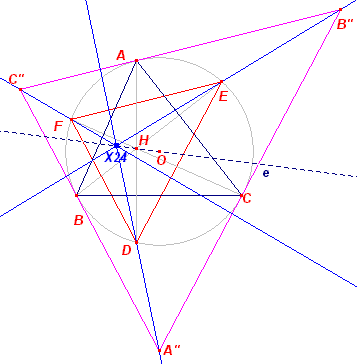
Gevolg van Stelling 2
Het homothetiecentrum X25 van A'B'C' en A"B"C" ligt op de Euler-lijn van driehoek ABC.

Bewijs:
Het punt H is het incentrum van de voetpuntsdriehoek A'B'C'; het punt O is het incentrum van A"B"C".
Onder de homothetie met X25 als centrum gaat H dus over in O.
X25 ligt dus op de lijn HO, de Euler-lijn van driehoek ABC. ¨

Stelling 3
Het middelpunt van de omcirkel van de raaklijnendriehoek van ABC ligt op de Euler-lijn van ABC.

Bewijs:

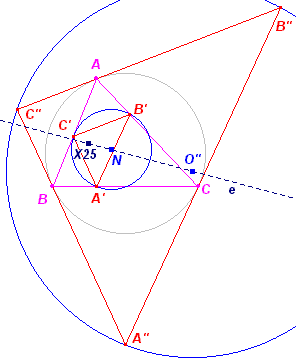gob3 Onder de in Stelling 2 gevonden homothetie (met centrum X25) gaat de omcirkel van A'B'C' (de negenpuntcirkel van ABC) over in de omcirkel van A"B"C".

Het middelpunt N van die negenpuntscirkel ligt op de Euler-lijn, X25 (het centrum van de homothetie) ligt ook op de Euler-lijn (zie Gevolg van Stelling 2).
Het beeld van N onder de bedoelde homothetie, zijnde het middelpunt O" van de omcirkel van A"B"C" (de raaklijnendriehoek), ligt dus eveneens op de Euler-lijn. ¨

Opmerking
Het punt O"  is het punt dat in de codering van Kimberling wordt aangeduid met X26.
[einde Opmerking]

3. En meer... terug

gob4
Definitie
De omcirkelhoogtepuntsdriehoek (Eng. circum-pedal triangle) van een driehoek is de driehoek gevormd door de snijpunten van de hoogtelijnen van de driehoek met de omcirkel.
Driehoek DEF in de figuur hiernaast is de omcirkelhoogtepuntsdriehoek van ABC.
.
Stelling 4
De omcirkelhoogtepuntsdriehoek en de hoogtepuntsdriehoek zijn gelijkstandig.

Bewijs:
OA is middelloodlijn van EF, bg(AE)  is immers gelijk aan bg(AF) (zie Stelling 1.2) en volgens Stelling 1.1 staat OA loodrecht op B'C', zodat
B'C" // EF, enz.
De beide driehoeken zijn dus gelijkstandig. ¨

Opmerking
Het centrum is in dit geval het punt H, het hoogtepunt van ABC.
[einde Opmerking]
gob4b
Gevolg van Stelling 4
[1] De raaklijnendriehoek en de omcirkelhoogtepuntsdriehoek van een driehoek zijn gelijkstandig.
[2] Het gelijkvormigheidspunt ligt op de Euler-lijn van de basisdriehoek.

Bewijs:
Het gestelde volgt onmiddellijk uit Stelling 2 en Stelling 4: (st2:) de hoogtepuntsdriehoek kan door een homothetie worden afgebeeld op de raaklijnendriehoek, en (st4:) de hoogtepuntsdriehoek kan door een homothetie worden afgebeeld op omcirkelhoogtepuntsdriehoek.
Omdat de centra van deze homothetieën (X25, zie het Gevolg van Stelling 2, en het punt H) op de Euler-lijn liggen, ligt ook het centrum van de homothetie die de omcirkelvoetpuntsdriehoek afbeeldt op de raaklijnendriehoek, op de Euler-lijn. ¨

Opmerking
Het homothetiecentrum is het punt dat in de codering van Kimberling wordt aangeduid met X24.
[einde Opmerking]
.
Stelling 5
De excentra van de raaklijnendriehoek vormen een driehoek die gelijkstandig is met de basisdriehoek.
Het omcentrum van de basisdriehoek is hoogtepunt van deze nieuwe driehoek.

Bewijs:

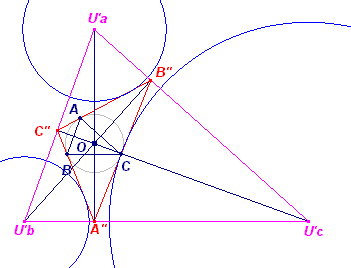gob5 In de figuur hiernaast is U'aU'bU'c de uitcentrumdriehoek van A"B"C".

Het punt O (het omcentrum van ABC) is het incentrum van A"B"C", de raaklijnendriehoek,. De lijnen OA", ... zijn dus de bissectricces van A"B"C".
Wegens de definitie van de uitcentrumdriehoek is nu OA" _|_ U'bU'c.
Verder is, vanwege A"B = A"C, ook: OA" _|_ BC.
We vinden dus BC // U'bU'c, ....
De driehoeken ABC en U'aU'bU'c zijn dus homothetisch.
De lijn OA" (binnenbissectrice van A"B"C") gaat ook door U'a.
U'aA" is dus hoogtelijn van U'aU'bU'c, ...

Dus O is hoogtepunt van U'aU'bU'c. ¨

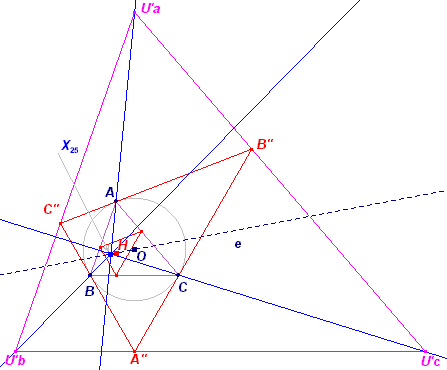gob5b Gevolg van Stelling 5
A"B"C" is hoogtepuntsdriehoek van U'aU'bU'c.
Het homothetisch verband tussen de hoogtepuntsdriehoek van ABC en de raaklijnendriehoek is hetzelfde als tussen de ABC en U'aU'bU'c.
Het gelijkvormigheidscentrum is dus eveneens het punt X25 (zie Stelling 2).
[einde Gevolg]
Stelling 6
De hoogtepuntsdriehoek van het hoogtepunt tov. de hoogtepuntsdriehoek is een driehoek die gelijkstandig is met de basisdriehoek.
Het homothetiecentrum is X25.

Bewijs:

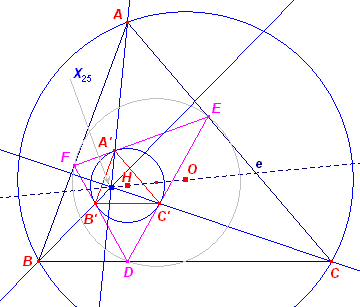gob6 In de figuur hiernaast is DEF de hoogtepuntsdriehoek bij ABC, en A'B'C' is de hoogtepuntsdriehoek van H tov. DEF.

EF is antiparallel met BC.
B'C' is antiparallel met EF.
Hieruit volgt dat BC // B'C', enz.
A'B'C' en DEF zijn dus gelijkstandig.

Zie verder Stelling 2 en Stelling 3. ¨

Opmerking
Stelling 6 is eigenlijk niets anders dan Stelling 5. Vergelijk de figuren!
[einde Opmerking]

4. Referenties terug

Zie ook de pagina "Bijzondere punten van de driehoek" (Kimberling-codering van punten op deze website).
Zie ook de pagina "Meer over isogonale verwantschap" (oa. over de antivoetpuntsdriehoek).

[1]    QUIM CASTELLSAGUER: TTW (Tot Triangles Web)
[2] ROGER A. JOHNSON: Advanced Euclidean Geomtery, Dover Publications (reprint, New York, 1960)
[3]   CLARK KIMBERLING: Triangle Centers and Central Triangles (TCCT), Utilitas Mathematical Publishing Inc. (Winnipeg, Canada, 1998)
[4] CLARK KIMBERLING: Encyclopedia of Triangle Centers - ETC (website)

begin pagina
[gob.htm] laatste wijziging op: 14-06-03