Cosinusregel (2)

Twee bewijzen ][ Cosinusregel (1) | Sinusregel | Analyse | Meetkunde

Twee bewijzen

Bewijs op basis van de stelling van Ptolemaeus
Bewijs gebaseerd op de macht van een punt tov. een cirkel

1. Bewijs op basis van de Stelling van Ptolemaeus

De stelling van Ptolemaeus luidt:
In een koordenvierhoek is het product van de diagonalen gelijk aan de som van de producten van de overstaande zijden.

We gaan uit van een bijzondere koordenvierhoek, nl. een gelijkbenig trapezium.

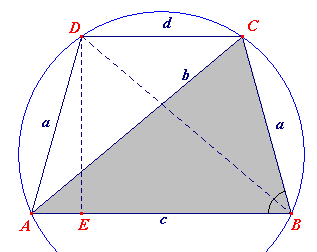ABCD is een gelijkbenig trapezium, met opvolgend zijden c, a, d, a, waarbij verder c > d.
Verder is AC = BD = b.
Zoals bekend is een gelijkbenig trapezium een koordenvierhoek.
Nu is ook:
   AE = AD cos B = a cos B
en dus ook d = c - 2a cos B
Dus geldt volgens de stelling van Ptolemaeus:
   b·b = a·a+ c·d = a·a + c(c - 2a cos B)
of
   b² = a² + c² - 2ac cos B

2. Bewijs gebaseerd op de macht van een punt tov. een cirkel

Zie de pagina "Macht van een punt tov. een cirkel"

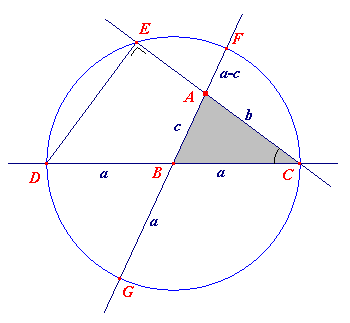Uitgaande van een willekeurige driehoek ABC construeren we de cirkel (B, BC).
CB snijdt die cirkel in D en CA snijdt die cirkel in E. AB snijdt de cirkel in de punten F, G.
Dan is cos C = CE / CD, zodat CE = 2a cos C.
Voor de macht van A tov. de cirkel hebben we:
   AF · AG = AC · AE
of
   (a - c)(a + c) = b(2a cos C - b)
   a² - c² = 2ab cos C - b²
zodat
   c² = a² + b² - 2ab cos C

Opmerking
Zie de pagina "Cosinusregel (1)" voor een ander bewijs op basis van de macht van een punt.
[einde Opmerking]

[p: cosinusregel.htm] laatste wijziging op: 20-10-2008 (27-12-2004)