Cirkelschijven
Overzicht ][ CabriPlus | Cabri | Meetkunde
1. Meetkundige plaats
van een meetkundige plaats ![]()
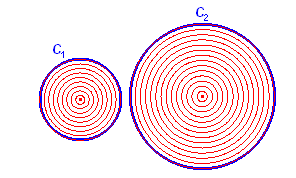
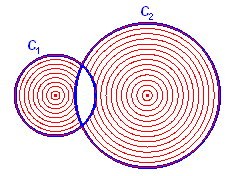
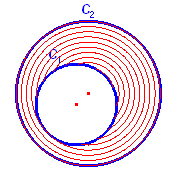
We beschouwen de cirkels C1 en C2 als cirkelschijven en willen de
verzameling punten arceren die binnen de ene cirkel liggen, maar niet binnen de andere;
dus het symmetrisch verschil van beide cirkelschijven:
C1 D C2 = (C1 È C2 ) \ (C1 Ç C2)
 |
 |
 |
We kunnen dit in CabriPlus realiseren met behulp van de daarin uitgebreide
functie "Meetkundige plaats".
Het is namelijk mogelijk direct de meetkundige plaats van een meetkundige plaats te
construeren.
We illustreren de bedoelde arcering (via cirkels) eerst met behulp van een CabriJavapplet (in Cabri Geometry II).
| Op het lijnstuk MX is een willekeurig punt P gekozen. Als X zich over de cirkel (M) beweegt, doorloopt het punt P eveneens een cirkel. Wanneer we nu in CabriGeometry II (Cabri II) in staat zouden zijn de meetkundige plaats van die cirkel te bepalen, dan krijgen we een arcering van de cirkelschijf die als uitgangspunt van bovenbedoelde arcering zou kunnen dienen. Echter, dat is in Cabri II niet mogelijk. We kunnen eea. in Cabri II (en dus in een CabriJavapplet) wel simuleren via de optie 'Spoor'. - Verschuif daartoe in nevenstaande applet het punt Spoor naar rechts. - Dubbelklik, indien gewenst, in het venster om het getekende spoor te wissen
We zullen in hetgeen volgt de constructiestappen van een macro voor CabriPlus
weergeven. |
We gaan uiteraard uit van twee cirkels met middelpunten M1 en M2
(de namen van de cirkels zijn C1 en C2).
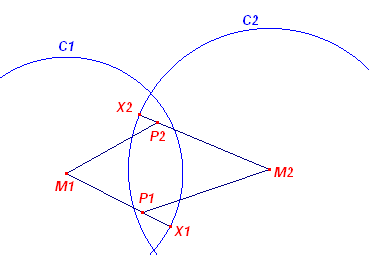
- We kiezen op C1 het punt X1 en op C2 het punt X2
- We kiezen op lijnstuk M1X1 het punt P en op lijnstuk M2X2
het punt P2.
- We bepalen het snijpunt S1 van M2P1 met cirkel C2.
- We bepalen het snijpunt S2 van M1P2 met met cirkel C1.
- Vervolgens tekenen we de halve lijnen M1S2 en M2S1.
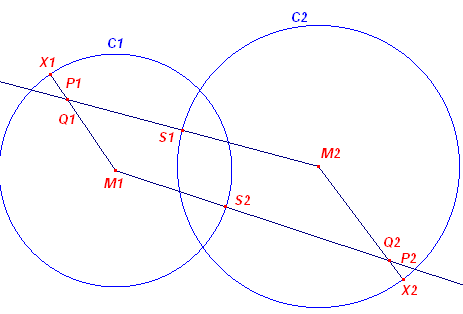
- Q1 = M2S1 /\ M1X1. Hier
betekent "/\": het snijpunt van .. en ..
- Q2 = M1S2 /\ M2X2
Nb.
Het punt Q1 bestaat alleen als P1
buiten cirkel C2 ligt (Q2 bestaat alleen als P2 buiten C1
ligt). Zie onderstaande figuur.
- De meetkundige plaats V1 van Q1 (bij variabele X1)
is nu het deel van de cirkel (M1, M1P1) dat binnen C1
ligt.
- De meetkundige plaats V2 van Q2 (bij variabele X2) is
nu het deel van de cirkel (M2, M2P2) dat binnen C2
ligt.
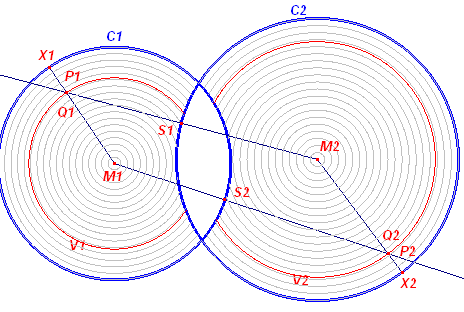
De meetkundige plaats van V1 (bij variabele P1) is
nu de gewenste arcering binnen C1.
De meetkundige plaats van V2 (bij variabele P2) is nu de gewenste
arcering binnen C2.
Macrodefinitie - Kies de beide cirkels als Beginobjecten en de beide meetkundige plaatsen (die van V1 en die van V2) als Eindobjecten. Het is daarbij aan te raden C1 en C2 'dik' te maken.
3.
Macro:D1(AND)D2.MAC ![]()
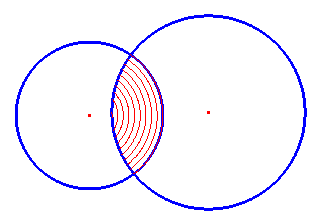
Min of meer hetzelfde principe (als in de vorige paragraaf) kan worden
toegepast om de punten van het gemeenschappelijk deel van twee cirkelschijven C1
en C2 te arceren (weer via cirkelbogen); de doorsnede van C1
en C2:
C1 Ç C2
 |
 |
We gaan uit van twee cirkels C1 en C2 (met
middelpunten M1 en M2)
- Kies het punt X op C1 en teken het lijnstuk M1X.
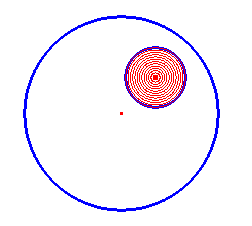
- Kies dan het punt P (wllekeurig) op M1X. Nb. Verplaats X
en/of P zo, dat P binnen C2 ligt.
- Bepaal met de functie "Inverse" het inverse punt P' van P ten opzichte van de
cirkel C2.
- Teken het lijnstuk P'C2 (dat door P gaat).
- Bepaal het snijpunt S van P'C2 met C2.
- Teken het lijnstuk SC2.
- Bepaal vervolgens het snijpunt Q van de lijnstukken SC2 en M1X. (P
en Q vallen dus in principe samen)
Nb.
Het punt Q bestaat alleen als het punt P binnen beide
cirkels ligt.
- Construeer de meetkundige plaats V van het punt Q (bij variabele X).
- Construeer de meetkundige plaats van V (bij variabele P).
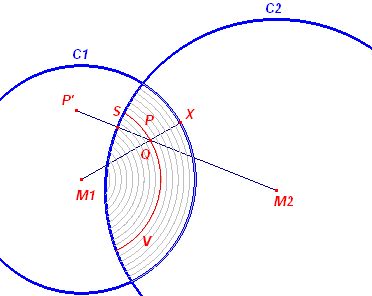
Macrodefinitie - Kies de cirkels C1 en C2 als Beginobjecten; kies de meetkundige plaats van V (de arcering) als Eindobject. Ook hier is het aan te raden de cirkels C1 en C2 'dik' te maken.
4.
Download ![]()
De hierboven beschreven CabriPlus macro's, alsmede de CabriPlus
figuren die bij de definitie daarvan zijn gebruikt, kunnen in één bestand worden
gedownload via deze website.
In het bestand is ook de figuur (voor Cabri II met extensie .fig1)
opgenomen die gebruikt is bij de CabriJavapplet.
Klik hier om het downloaden te starten
(ZIP-bestand; ca. 5 Kb).
Met dank aan Joseph Hornière (www.dino-optic.com, La PAGE-MAISON consacrée à l'Optique, Frankrijk).