Stelling van Casey

Inleiding | Bewijs | Omgekeerde steling  ][  Inversie | Ptolemaeus | Meetkunde

1. Inleiding
De bedoelde stelling luidt:

Stelling van Casey
Raken vier cirkels C1, C2, C3, C4 alle uitwendig aan dezelfde cirkel C,  dan is
   t13t24 = t12t34 + t14t23 
waarbij t ij de lengte is van het uitwendige gemeenschappelijk raaklijnstuk van de cirkels Ci en Cj .
figuur 1  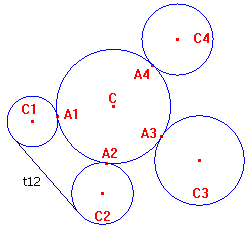casey1

Bij het bewijs van de stelling gebruiken we de volgende

Hulpstelling
Is t het gemeenschappelijk raaklijnstuk van twee cirkels met stralen r1 en r2, dan is het getal  c = t / Ö(r1r2) invariant bij inversie.

Bewijs: zie figuur 2.

figuur 2  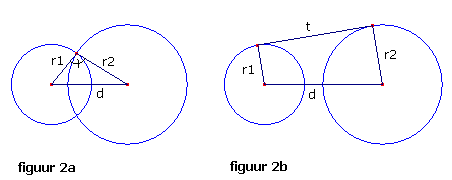casey2

In de driehoek in figuur 2a geldt in de driehoek (volgens de cosinusregel):
   d2 = r12 + r22 - 2r1r2 cos j
Dus:
   imagescasey_f1
De uitdrukking voor z heeft ook betekenis als de beide cirkels elkaar niet snijden (z is dan natuurlijk niet de cosinus van een reële hoek).
Bij inversie is de waarde van z invariant. Immers:
Kiezen we een punt van de machtlijn van de beide cirkels als centrum van inversie, en is m de macht van dat punt tov. beide cirkels en k de inversiemacht, dan is de gelijkvormigheidsfactor gelijk aan k2/m.
De uitdrukking voor z is homogeen kwadratisch. Waaruit het gestelde omtrent z volgt.

In figuur 2b is vinden we dan, samen met de uitdrukking voor z:
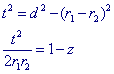
   imagescasey_f2
z verandert niet bij inversie, dus ook c = t / Ö(r1r2) verandert niet bij inversie. ¨

2. Bewijs van de stelling
We geven een tweetal bewijzen:
   2.1. Bewijs met inversie
   2.2. Bewijs zonder inversie

2.1. Bewijs met inversie
Zie hiervoor figuur 3.

figuur 3  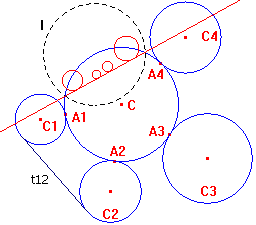casey3 De cirkel C gaat bij de inversie met inversiecirkel I, waarvan het middelpunt op C ligt over in een rechte lijn, waaraan de 4 beeldcirkels van Ci raken.
De raakpunten  zijn Ai' en de stralen van deze cirkels ri'.

Volgens de stelling van Ptolemaeus geldt in vierhoek A1A2A3A4:
   A1A3 . A2A4 = A1A2 . A3A4 + A1A4 . A2A3
Dit geldt dus ook voor de geacccentueerde punten Ai'.
Voor de lijnstukken A1'A2' = t 12', .....
vinden we dan, na deling door  Ö(r1'r2'r3'r4'):

   imagescasey_f3
Wegens de invariantie van tij' / Ö(ri'rj') -zie de hulpstelling in paragraaf 1- is dus, bij vermenigvuldiging met Ö(r1r2r3r4)
   t13t24 = t12t34 + t14t23
waarmee de stelling bewezen is. ¨

Opmerking
De stelling van Casey is heeft de stelling van Ptolemaeus als bijzonder geval, namelijk als r1= r2= r3= r4 = 0.
[einde Opmerking]

2.2. Bewijs zonder inversie
Zie hiervoor figuur 4.

figuur 4  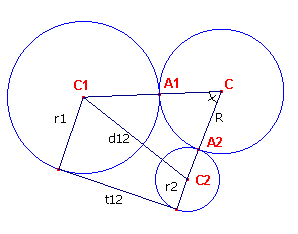casey4 We bekijken de cirkels C (straal R), C1 (straal r1) en C2 (straal r2).
We stellen C1C2 = d12 en hoek C1CC2 = j.

Nu is
(1)   (t12)2 = (d12)2 - (r1-r2)2
(2)   (d12)2 = (R+r1)2 + (R+r2)2 - 2(R+r1)(R+r2)cos j
(3)   (A1A2)2 = 2R2(1-cos j)
Na enige herleiding vinden we hieruit
   imagescasey_f4
Voor de andere raaklijnstukken vinden we overeenkomstige uitdrukkingen.

De stelling van Casey volgt nu door toepassing van de stelling van Ptolemaeus, met gebruikmaking van bovenstaande uitdrukkingen voor t12, t13, ..... , t34 op de koordenvierhoek A1A2A3A4. ¨

3. Omgekeerde stelling
De omgekeerde stelling van Casey (we geven deze zonder bewijs) geldt eveneens. Dus:

Stelling
Als voor vier cirkels C1, C2, C3, C4 geldt
    t13t24 = t12t34 + t14t23  
waarbij t ij de lengte is van het uitwendige gemeenschappelijk raaklijnstuk van de cirkels Ci en Cj ,
dan raken de vier cirkels  alle uitwendig aan dezelfde cirkel C.

Maar er kan ook sprake zijn van inwendige raking van een of meer van de cirkels Ci aan de cirkel C. Ook in dit geval blijft de stelling geldig.
Echter, met moet dan bij twee elkaar op verschillende wijze rakende cirkels de uitwendige raaklijn t ij vervangen door de inwendige gemeenschappelijk raaklijn v ij.
Als t (respectievelijk v) niet bestaat kunnen we toch, als hierboven (in het bewijs zonder inversie) de uitdrukking (1) gebruiken:
   (t12)2 = (d12)2 - (r1-r2)2 
Er treden dan echter wel ingewikkelde tekenkwesties op in de algemene formulering:

   t12t34 ± t13t24 ± t14t23 = 0  

We kunnen dan een bijzonder gevolg van de omgekeerde stelling formuleren, namelijk de stelling van Feuerbach.

Gevolg

Stelling (stelling van Feuerbach)
Als C1, C2, C3 de uitcirkels zijn van een driehoek en C4 is de incirkel van die driehoek, dan is er een cirkel C, waaraan C1, C2, C3 uitwendig en C4 inwendig raakt.

Bewijs:
Voor de in- en aangeschreven cirkels van de driehoek met zijden a, b, c geldt:
t 12 = a + b, v 34 = a - b, ..... .
Nu hebben we
   imagescasey_f5
waaruit we volgens de algemeen geformuleerde omgekeerde stelling van Casey kunnen concluderen, dat er dus een cirkel C bestaat die inwendig aan C4 en uitwendig aan C1, C2, C3 raakt: de cirkel van Feuerbach (negenpuntscirkel)! ¨ 

begin pagina

[casey.htm] laatste wijziging op: 21-08-1999