Oppervlakken met CabriPlus
Overzicht ][ CabriPlus | Cabri | Meetkunde
- Oppervlak en assenstelsel
- Domein
- De ruimte in
- Meetkundige plaatsen
- Het oppervlak
- Enkele andere voorbeelden
1. Oppervlak en
assenstelsel ![]()
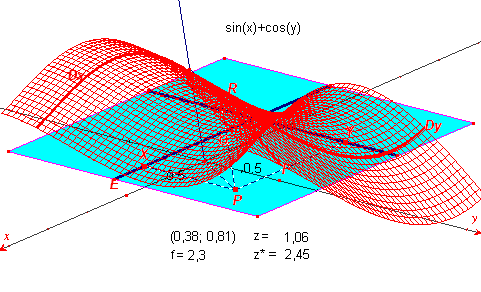
Uitgaande van, bijvoorbeeld, de volgende vergelijking
z = sin(x) + cos(y)
kunnen we met Cabri (Plus) een afbeelding van het oppervlak
creŰren.
We beschrijven eea. hieronder.
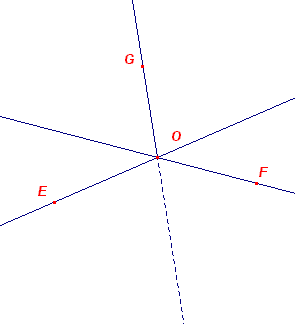
We kiezen twee elkaar in O snijdende lijnen op het tekenblad. Deze lijnen zullen
"dienst doen" als dragers van de x-as en de y-as.
Op elk van deze lijnen kiezen we een punt (zie E en F) dat de eenheid op elke as bepaalt.
We tekenen door O ook een derde lijn. Op deze lijn kiezen we een punt G, en door O en G
tekenen we een halve lijn.
Deze halve lijn zal dienen als z-as.
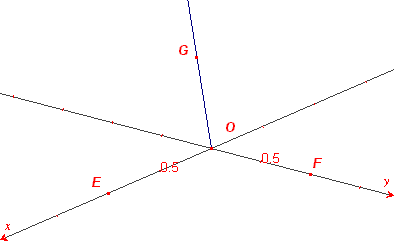
Met de functie "Nieuw assenstelsel" tekenen we de x-as en y-as,
bepaald door O, E en F.
 |
 |
2. Domein
![]()
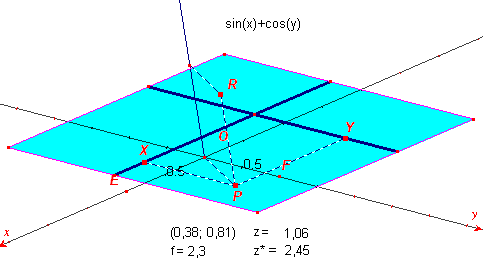
Voor het domein van de functie kiezen we twee lijnstukken, elk
evenwijdig aan een as (dit alleen om handiger met het domein en met punten te kunnen
manipuleren).
Met door de eindpunten van die lijnstukken gaande lijnen (evenwijdig met de assen) wordt
het domein zichtbaar in de tekening.
Kiezen we nu op beide lijnstukken een referentiepunt (X en Y), dan kunnen de co÷rdinaten
van elk punt P binnen het domein ten opzichte van het assenstelsel worden bepaald (met de
functie "Co÷rdinaten").

3. De ruimte in
![]()
Met de x- en y-coordinaat van P kunnen we nu de
waarde van z in de uitdrukking (Expressie) z = sin(x) +
cos(x) berekenen.
Ten einde een wat fraaiere figuur te verkrijgen kunnen we die waarde vermenigvuldigen met
een bepaalde factor f (dit geeft de waarde van z*).
De waarde van z* brengen we over op de z-as (de halve lijn door O en G).
En dan zijn we, op de gebruikelijke wijze, in staat een punt R van het oppervlak te
construeren!
4. Meetkundige plaatsen
![]()
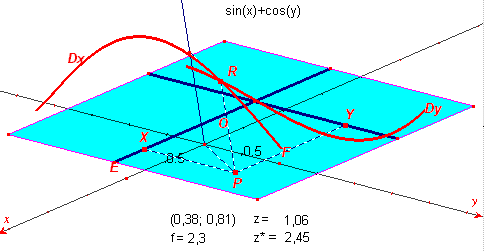
Wanneer we nu de meetkundige plaats van het punt R bepalen met X als
onafhankelijk punt, dan krijgen we een doorsnede van het oppervlak met een vlak y
= constant (ic. in bovenstaande figuur het vlak y = 0,81).
Wanneer we de meetkundige plaats van het punt R bepalen met Y als onafhankelijk punt, dan
krijgen we een doorsnede van het oppervlak met een vlak x = constant
(in casu x = 0,38).
Zie de kromme lijnen Dy en Dx (in onderstaande figuur).
5. Het oppervlak
![]()
Door nu van Dx de meetkundige plaats te bepalen met X als onafhankelijk punt,
en ook van Dy met Y als onafhankelijk punt, krijgen we een afbeelding van het oppervlak z = sin(x) + cos(y).
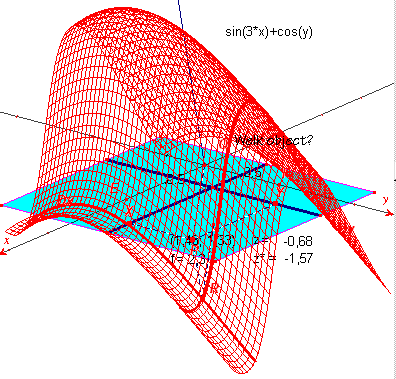
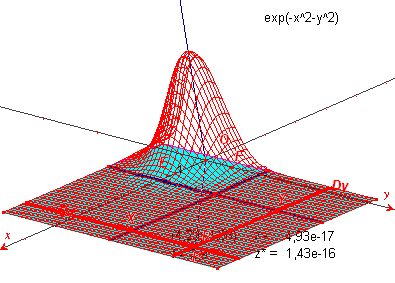
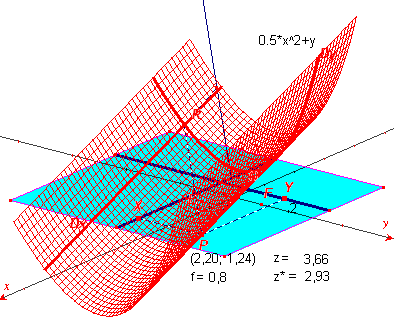
| z = sin(3x) + cos(y) | z = exp(- x2 - y2) | |
 |
 |
|
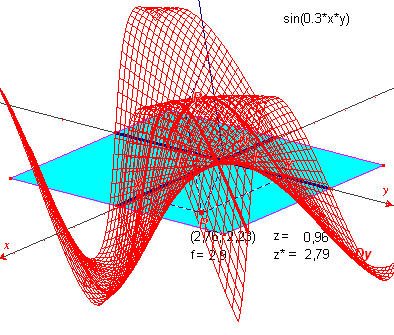
| z = sin(0,3xy) | z = 0,5x2 + y | |
 |
 |
Opmerking
Hierboven is specifiek gebruik gemaakt van de mogelijkheden die de functie
"Expressie" in CabriPlus biedt.
Eea. is ook mogelijk in Cabri II. Daarbij moet echter de Expressie
worden berekend worden via de Rekenmachine van Cabri.
De niveaulijnen kunnen dan slechts met behulp van "SpoorAan/Uit" worden
getekend.