Het Monge-punt van een viervlak

Overzicht ][ Cabri 3D | Overzicht stereo

Overzicht

Inleiding, stelling van Monge
Inderdaad, vier Monge-lijnen
Het Monge-punt bestaat
Opmerking mbt 12-punts- en 24-puntsbol van een viervlak
Cabri 3D applets
Download

1. Inleiding, stelling van Monge

figuur 1a

figuur 1b (als applet)

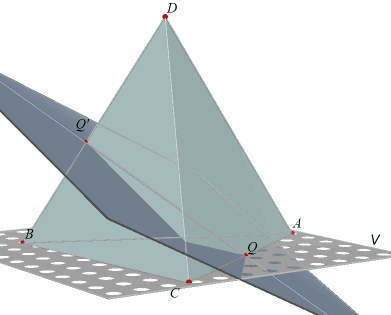
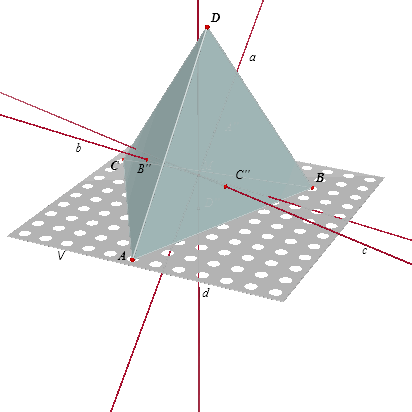
We hebben een willekeurig viervlak ABCD, waavan de punten A, B, C gelegen zijn in een vlak V.
De middens van de ribben AB, AC, AD, ... zijn opvolgend P, Q, R, ...
Die zes ribben geven dan ook zes ribbemiddens.

Definitie
Een loodvlak door zo'n ribbemidden op de overstaande ribbe van de ribbe waarop het ribbemidden gelegen is, heet een Monge-vlak (naar Gaspard Monge, 1746-1818, Frankrijk) van het viervlak (zie figuur 1a).

Er zijn dus ook zes Monge-vlakken.

Stelling van Monge
De zes Monge-vlakken van een viervlak gaan door hetzelfde punt, het zogenoemde Monge-punt van het viervlak.

In figuur 1b zijn de vier snijlijnen van de zes Monge-vlakken weergegeven.
Deze lijnen noemen we in hetgeen volgt Monge-lijnen.
En waarom zijn er maar vier Monge-lijnen? >>>

2. Inderdaad, vier Monge-lijnen

figuur 2 (als applet)

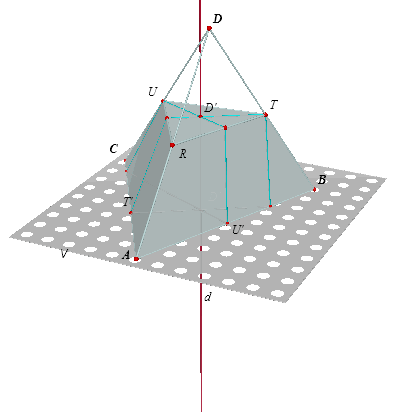We bekijken de middens R, T, U van de ribben DA, DB, DC.
De punten R, T, U liggen in een vlak dat evenwijdig is met vlak ABC (hiernaast, in figuur 2) ook aangegeven met V).
De snijpunten van de Monge-vlakken van T, U op de overstaande ribben zijn T' en U'.

Deze Monge-vlakken staan ook (opvolgend) loodrecht op RT, TU en UR, immers RT // AB, TU // BC, UR // CA.
De snijlijnen van deze Monge-vlakken met het vlak RTU zijn dus de hoogtelijnen van driehoek RTU, die elkaar snijden in het hoogtepunt D' van driehoek RTU.
Het punt D' ligt in die drie Monge-vlakken.
Aangezien die loodvlakken niet evenwijdig zijn, hebben ze dus (waarom hier 'dus'?) een gemeenschappelijke snijlijn: de Monge-lijn van het zijvlak ABC van het viervlak.
De Monge-lijn d van zijvlak ABC is dus de loodlijn D'D" uit D' op vlak ABC.

De Monge-vlakken snijden elkaar dus drie aan drie in dezelfde lijn, of ook
er zijn dus inderdaad vier Monge-lijnen (zie figuur 1 en applet 4).

We zullen nu aantonen, dat de vier Monge-lijnen door hetzelfde punt M gaan. >>>

3. Het Monge-punt bestaat

figuur 3a (als applet)
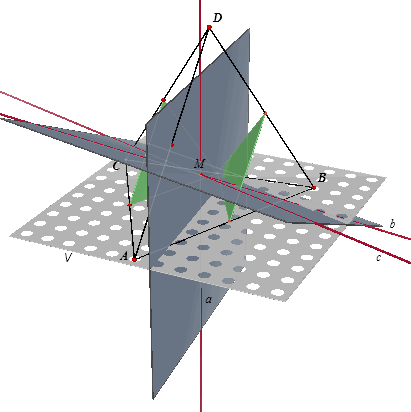	In figuur 3a zijn ook de Monge-lijnen b en c (van opvolgend ACD en ABD) getekend. De lijn b staat loodrecht AD (b staat immers loodrecht op ACD) en de lijn c staat ook loodrecht op AD (c staat immers loodrecht op ABD). Ze liggen beide in het Monge-vlak op AD en zijn niet evenwijdig. De lijnen b en c snijden elkaar dus. Stel dit snijpunt is M. Via een analoge redenering kunnen we aantonen, dat ook de lijn a door M gaat We zullen aantonen dat ook de lijn d door M gaat. Omdat het punt M in de Monge-vlakken op ... en ... ligt, ligt M ook op de snijlijn van die vlakken. De snijlijn van is echter de lijn d. M ligt dus in elk van de zes Monge-vlakken. Hiermee is de stelling van Monge bewezen.¨
figuur 3b
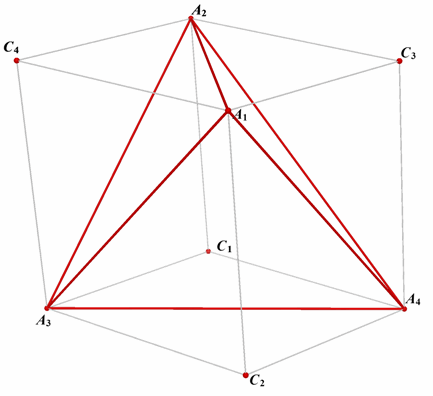	Opmerking Het Monge-punt kan ook worden bekeken vanuit het zogenoemde omgeschreven blok van een viervlak (zie figuur 3b). Het omgeschreven blok is het blok dat wordt gevormd door de vlakken door een ribbe van het viervlak evenwijdig met de overstaande ribbe daarvan. Deze manier van benaderen wordt gebruikt in het artikel "Over het Monge-punt van een viervlak en over enkele bollen". Ook worden daarin de 'Monge-eigenschappen' van een orthogonaal viervlak besproken (oa. de 24-puntsbol en de 12-puntsbol). ¤ Klik hier voor een PDF-bestand (ca. 375 kB) met dit artikel. Dit bestandsformaat is te lezen met Adobe^® Reader. Klik hier >< om Adobe Reader, indien gewenst, te downloaden. [einde Opmerking]

4. Cabri 3D applets
Bovenstaande figuren kunnen bekeken worden via een Cabri 3D applet.
Hiertoe is het noodzakelijk dat het programma Cabri 3D op het gebruikte systeem geïnstalleerd is (als plug-in van de gebruikte browser; klik hier voor informatie over de Cabri 3D plug-in).
Alle applets worden getoond in een NieuwVenster van de browser!

1. Klik hier >< voor de applet bij figuur 1b.
2. Klik hier >< voor de applet bij figuur 2.
3. Klik hier >< voor de applet bij figuur 3.
4. Klik hier >< voor een applet met de zes Monge-vlakken (automatisch draaiiend).

5. Download
De gebruikte Cabri 3D bestanden kunnen via deze website worden gedownload.
Klik hier om het downloaden te beginnen (ZIP-bestand; ca. 40 kB).

[p : mongepunt.htm] laatste wijziging op: 05-10-2005