Benadering van p via de Naaldproef van Buffon

Beschrijving | Uitvoering met grafiek | Uitvoering zonder grafiek  ][  Overzichtspagina | Meetkunde

Een MapleV-worksheet - september 1998 (klik hier om de worksheet [ZIP-bestand, 14Kb] te downloaden)
naar een idee van Michael Schmitz
Friedrich-Schiller-Universität Jena
Fakultät für Mathematik und Informatik

1. Beschrijving
De benadering van p die hieronder wordt beschreven is voor het eerst uitgevoerd door de Franse wiskundige George Buffon (George Louis Leclerc Comte de Buffon, 1707-1788).
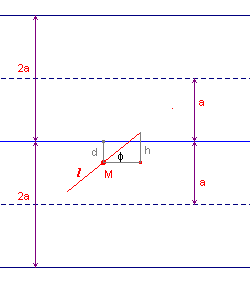
Deze wijze van benadering staat bekend als de Naaldproef van Buffon.

figuur 1  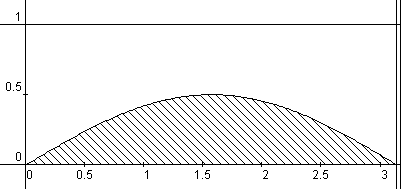benpi1-1 Op een stuk papier worden evenwijdige lijnen getekend elk op een afstand 2a van elkaar. Vervolgens wordt er bij herhaling een "naald" met lengte 2l, waarbij a groter is dan l, willekeurig op het papier geworpen, waarbij het aantal keren, dat de naald een punt gemeen heeft met een lijn wordt geteld (we noemen zo'n situatie een "treffer").
Voor de theoretische behandeling van de naaldproef is het voldoende de situatie bij slechts een enkele lijn te bekijken.
We nemen verder aan, dat het midden M van de naald bij de beschouwde lijn een afstand d tot die lijn heeft van ten hoogste a (zie de figuur).

Nu geldt h = lsin( f ), waarbij er sprake is van een treffer, indien h <= a.
Aan elke naaldworp voegen we nu het geordende paar (f, a) toe en tekenen dat paar als punt in een  f-a-coördinatenstelsel.

figuur 2  benpi1-2

Dan liggen de punten die bij een treffer horen in het vlakdeel dat door de  f-as en de grafiek van de functie a = lsin( f ) met 0 £ f £ p begrensd wordt (en omgekeerd).
Punten die bij worpen horen die niet tot een treffer leiden, liggen buiten dat vlakdeel, maar behoren wel tot de in de figuur getekende rechthoek met zijden a en p (in figuur 2 is a = 1 en l = 1/2) .
Uit de waarschijnlijkheidsrekening volgt nu dat de verhouding tussen het aantal treffers en het aantal worpen gelijk is aan de verhouding tussen de oppervlaktes van het vlakdeel dat begrensd wordt door de grafiek van a = lsin( f ) en de  f-as en van de rechthoek met zijden p en a.
Dus
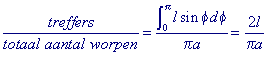
   imagesbenpi1-f1
waaruit nu eenvoudig volgt dat
   imagesbenpi1-f2
Kiezen we nu l = a/2  (zie ook figuur 2), dan kunnen we de waarde van p , onafhankelijk van de lengte van de naald en de afstand tussen de lijnen, berekenen uit
   imagesbenpi1-f3

2. Uitvoering met grafiek
We gooien 100 keer met een naald (zie de variabele "aantal").

> restart:
> with(plots):
> aantal:=100:

Voor het model gaan we uit van een x-y-coördinatenstelsel.
We bekijken twee lijnen met vergelijkingen y = 1 en y = 3.
De worpen leggen we nu zo vast, dat het midden M(x, y) van de naald zo terecht komt, dat   0 £ x £ 5 en 0 £ y £ 4 .
Daarbij geldt a = 1 en l = 1/2.

We berekenen eerst de x-coördinaten van het midden M van de naald. Deze moeten liggen tussen 0 en 5:

> coor_x:=[]:
> for N from 1 to aantal do
>   Zx:=evalf(rand(50000)/10000):
>   coor_x:=[op(coor_x),Zx()]:
> od:

Opmerking
De Maple-opdracht rand( ) wordt toegelicht op de pagina "Benadering van Pi met oppervlaktes".
[einde Opmerking]

Vervolgens de y-coördinaten van M die tussen 0 en 4 moeten liggen.

> coor_y:=[]:
> for N from 1 to aantal do
>   Zy:=evalf(rand(40000)/10000):
>   coor_y:=[op(coor_y),Zy()]:
> od:

En tenslotte de grootte van de hoek f .
Daartoe bepalen we toevalsgetallen die liggen tussen 0 en 180 (graden), die omgerekend worden naar radialen.

> hoek := []:
> for N from 1 to aantal do
>   Zh:=evalf(rand(180)*Pi/180):
>   hoek:=[op(hoek),Zh()]:
> od:

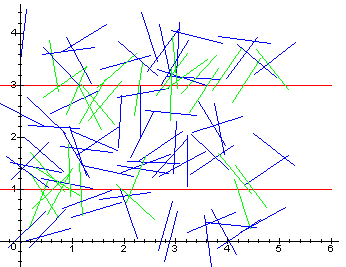
We kijken nu hoe de worpen zijn uitgevallen. We tekenen ze in een figuur (zie figuur 3), waarbij de groene lijnstukken treffers zijn. De blauwe lijnstukken hebben hun "doel" gemist.

> l:=0.5:
> lijn1:=plot([[-1,1],[6,1]],color=red):
> lijn2:=plot([[-1,3],[6,3]],color=red):
> naalden:=[lijn1,lijn2]:
> treffers:=0:
> for i from 1 to aantal do
>   if (abs(coor_y[i]-1)<=l*sin(hoek[i]) or 
>       abs(coor_y[i]-3)<=l*sin(hoek[i])) then  
>     naald:= plot(
>             [[coor_x[i]-(l*cos(hoek[i])), coor_y[i]-(l*sin(hoek[i]))],
>              [coor_x[i]+(l*cos(hoek[i])), coor_y[i]+(l*sin(hoek[i]))]], 
>             color=green):
>     treffers:=treffers+1:
>   else
>     naald:=plot(
>            [[coor_x[i]-(l*cos(hoek[i])),coor_y[i]-(l*sin(hoek[i]))],
>             [coor_x[i]+(l*cos(hoek[i])),coor_y[i]+(l*sin(hoek[i]))]],
>            color=blue):
>      fi:
>   naalden:=[op(naalden),naald]:
> od:
> Aantal:=aantal;
> AantalTreffers:=treffers;
> Benadering:=evalf(aantal/treffers);
> display(naalden, scaling=constrained);
Aantal := 100
AantalTreffers := 31
Benadering := 3.225806452

figuur 3 

benpi1-3

3. Uitvoering zonder grafiek
Dezelfde berekening zonder het tekenen van de lijnstukken verloopt natuurlijk wat sneller.
De waarden van x (coor_x), y (coor_y) en phi (hoek) zijn hetzelfde als in paragraaf 2.
De waarde van de benadering van p dus eveneens.

> treffers:=0:
> for i from 1 to aantal do
>   if (abs(coor_y[i]-1)<=l*sin(hoek[i]) or 
>       abs(coor_y[i]-3)<=l*sin(hoek[i])) then  
>     treffers:=treffers+1:
>   fi:
> od:
> Aantal:=aantal;
> AantalTreffers:=treffers;
> Benadering:=evalf(aantal/treffers);
Aantal := 100
AantalTreffers := 31
Benadering := 3.225806452

begin pagina

[benpi1.htm] laatste wijziging op: 15-10-1999