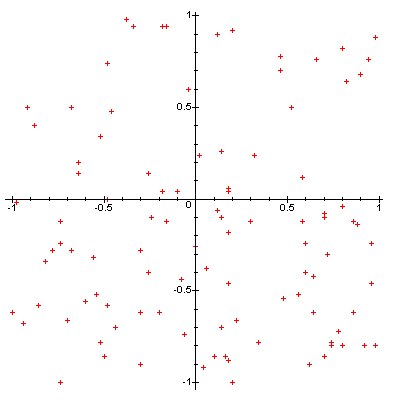Benadering van p via oppervlakte-bepaling

Beschrijving | Toevalsgetallen | Benadering | Andere methode  ][ Overzichtspagina | Meetkunde

Een MapleV-worksheet - februari 1998 (klik hier om de worksheet [ZIP-bestand, 10Kb] te downloaden )
naar een idee van Michael Schmitz
Friedrich-Schiller-Universität, Jena
Fakultät für Mathematik und Informatik

1. Beschrijving
In Maple is het mogelijk met behulp van de opdracht rand( ) toevalsgetallen te genereren (zie paragraaf 2). Daarmee kan dan een benadering van het getal p worden gevonden

figuur 1

We gaan uit van een vierkant met zijde 2r met ingeschreven cirkel (zie figuur 1). We kiezen binnen dat vierkant willekeurig een aantal punten. De verhouding tussen het aantal punten binnen de cirkel en het aantal punten buiten de cirkel geeft een benadering van p, gebaseerd op de oppervlakte van de beide vlakdelen. We hebben namelijk:

Daaruit volgt dan:

Opmerking
In het bovenstaande is met "punten" steeds bedoeld "punten liggend binnen het vierkant".
[einde Opmerking]

2. Genereren van toevalsgetallen
Toevalsgetallen verkregen met de Maple-opdracht rand( ) zijn gehele getallen liggend uit het interval [1 ; 10¹² - 1]; het zijn dus maximaal 12 cijferige getallen.
De opdracht W := rand(n) kent aan W een procedure toe die een toevalsgetal oplevert uit het interval [0 ; n-1].
De opdracht W := rand(a..b) kent aan W een procedure toe die een toevalsgetal oplevert uit het interval [1 ; b]
W is dus geen variabele, maar een procedure.
W moet worden aangeroepen met W( ).

Voorbeeld
We genereren 40 toevalsgetallen uit de verzameling {0, 1, 2, 3, 4}, die we opnemen in een rij Z₁:

> restart:
> Z1 := []:
> W := rand(5):
> for N from 1 to 40 do
>   Z1 := [op(Z1),W()]:
> od:
> Z1; 

[1, 0, 2, 3, 1, 3, 0, 3, 1, 4, 0, 3, 2, 0, 4, 0, 1, 1, 2, 4, 1, 3, 1, 4,
 3, 1, 4, 1, 3, 2, 1, 3, 0, 1, 3, 3, 0, 4, 0, 1]

[einde Voorbeeld]

Willen we echter gebruik maken van getallen met 5 decimalen die in het interval ] -1 ; 1 [ liggen, dan moeten we de hieronder beschreven, voor de hand liggende, werkwijze toepassen.
We genereren 15 van deze getallen.

> Z2 := []:
> W := evalf(2*rand(100000)/100000,1)-1:
> for N from 1 to 15 do
>   Z2 := [op(Z2),W()]:
> od:
> Z2;

[-.82410, .10948, .48618, -.37280, -.83236, .51184, .77226, .34554, 
  .87498, -.43330, -.97478, .41096, .68006, -.88154, -.87610]

We gebruiken de random-generator vervolgens om de coördinaten (in twee decimalen) van 100 punten te generenen die binnen een om de oorsprong beschreven vierkant met zijde 2 liggen.
Deze punten worden daarna geplot in dat coördinatenstelsel (zie figuur 2).

> punten := []:
> x := evalf(2*rand(100)/100,1)-1:
> y := evalf(2*rand(100)/100,1)-1:
> for N from 1 to 100 do
>   punten:=[op(punten),[x(),y()]]:
> od:
> plot(punten, style=point);

figuur 2

3. Benadering van p
Voor de benadering kiezen we de eenheidscirkel met het omgeschreven vierkant en vervolgens gebruiken we toevalsgetallen uit het interval ]-1 ; 1[.

figuur 3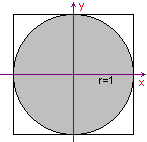

Voor een eerste onderzoek gaan we uit van 1000 punten..

> aantal := 1000;
> incirkel:=0:
> x := evalf(rand(2000)/1000,1)-1:
> y := evalf(rand(2000)/1000,1)-1:
> for n from 1 to aantal do
>   X := x():
>   Y := y():
>   if X^2+Y^2<1 then
>     incirkel := incirkel +1
>   fi:
> od:
> incirkel := incirkel;
> benadering := evalf(4*incirkel/aantal);

aantal := 1000
incirkel := 795
benadering := 3.180000000

Opmerking
De rekentijd bij 10.000 iteraties is ongeveer 180 seconden (Pentium, 100 MHz, 48 Mb RAM)
[einde Opmerking]

4. Een iets andere methode
We kunnen ook voor een iets andere opzet van de cirkels kiezen.
We gaan uit van 4 cirkels (zie figuur 4) in een vierkant met zijde 4.

figuur 4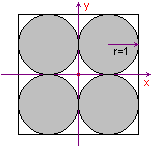

Een berekening in dit model geeft

> aantal := 1000;
> incirkel := 0:
> x:=evalf(rand(4000)/1000,1)-2:
> y:=evalf(rand(4000)/1000,1)-2:
> for n from 1 to aantal do
>   X:=x():
>   Y:=y():
>   if ( (X+1)^2+(Y-1)^2<1 or (X+1)^2+(Y+1)^2<1 or 
>        (X-1)^2+(Y+1)^2<1 or (X-1)^2+(Y-1)^2<1 ) then
>     incirkel := incirkel+1
>   fi:
> od:
> incirkel := incirkel;
> benadering:=evalf(4*incirkel/aantal);

aantal := 1000
incirkel := 783
benadering := 3.132000000

[benpi2.htm] laatste wijziging op: 27-12-2004