Anticomplementaire driehoek

Overzicht ][ Bijzondere punten | Meetkunde

Overzicht terug

  1. Naamgeving
  2. Een enkele eigenschap

1. Naamgeving terug
We geven de volgende definities (met een in Nederland niet-algemeen gebruikte naamgeving van bijzondere driehoeken).

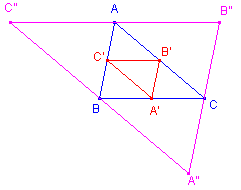acdrieh1
Definitie
[1] De centrumdriehoek van driehoek ABC is de driehoek met de middens van de zijden van ABC als hoekpunten (A'B'C').
[2] De anticomplementaire driehoek van driehoek ABC is de driehoek waarvan ABC de centrumdriehoek is (A"B"C").
[3] Driehoek ABC wordt in beide gevallen wel de referentiedriehoek genoemd.

Opmerkingen
[1] In plaats van 'centrumdriehoek' wordt ook wel gebruikt: zwaartepuntsdriehoek en centrale driehoek.
Een betere benaming zou wellicht middenparallel-driehoek zijn.
[2] In plaats van 'anticomplementaire driehoek' wordt ook wel gebruikt: anticentrumdriehoek en anticentrale driehoek.
[einde Opmerkingen]

2. Een enkele eigenschap terug
Bijna alle eigenschappen van de anticomplementaire driehoek kunnen worden afgeleid uit Stelling 1.

Stelling 1
Een driehoek en zijn anticomplementaire driehoek zijn perspectief, met Z als perspector.

Bewijs:

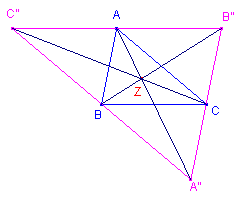acdrieh2 We beschouwen de vermenigvuldiging V met Z als centrum en factor k = -2.
Zij V(A) = A", V(B) = B", V(C) = C"
Uit de (bekende) eigenschapppen van de afbeelding V volgt nu : B"C" // BC, enz. Volgens de middenparallel-stelling zijn dan A, B, C de middens van de zijden van A"B"C"
A"B"C" is dus de anticomplementaire driehoek van ABC. ¨

Opmerking
De perspectief-as is de oneigenlijke rechte. Zie daarvoor eventueel ook de pagina "Absolute elementen..."
[einde Opmerking]
.
Stelling 2
Het hoogtepunt van de anticomplementaire driehoek ligt op de Euler-lijn van zijn referentiedriehoek.

Bewijs:

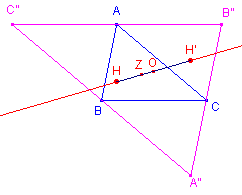acdrieh3 A"B"C" is de anticomplementaire driehoek van ABC.
De lijn OH is (per definitie) de Euler-lijn van driehoek ABC.
Het punt Z ligt hierop (zie de pagina "De stelling van Feuerbach").
Bij de vermenigvuldiging met k = -2 tov. Z ligt H' op OH.
De lijn AH is een hoogtelijn van ABC. Gevolg: A"H' _|_ B"C".
A"H' is dus hoogtelijn van A"B"C"; enz.
H' is dus hoogtepunt van A"B"C". ¨
 
Gevolg
H' is het beeld van H bij puntspiegeling in het punt O.

[einde Gevolg]

Opmerking
Het punt H' wordt wel het DeLongchamps-punt van driehoek ABC genoemd.
Zie de pagina "Bijzondere punten van een driehoek" - volgens Kimberling's TCCT: X20).
[einde Opmerking]

begin pagina
[acdriehoek.htm] laatste wijziging op: 01-09-02