Zwaartelijnen

Concurrente zwaartelijnen van een driehoek

Overzicht

Inleiding
Twee bewijzen met behulp van een middenparallel
Direct bewijs
Bewijs met oppervlaktes

1. Inleiding
Op de pagina "Transversalen" is met behulp van de Stelling van Ceva bewezen, dat de zwaartelijnen van een driehoek concurrent zijn.
We geven op deze pagina enkele wat meer traditionale bewijzen van de stelling:

Stelling
[1] De zwaartelijnen van een driehoek gaan door één punt.
[2] De zwaartelijnen van een driehoek delen elkaar in stukken die zich verhouden als 2 : 1.

We bewijzen allereerst een hulpstelling.

Hulpstelling
Het lijnstuk dat de middens van twee zijden van een driehoek verbindt, is evenwijdig met de derde zijde en gelijk aan de helft van de derde zijde.

Opmerking
De lijn door de middens van twee zijden van een driehoek is een middenparallel van die driehoek.
[einde Opmerking]

Bewijs:

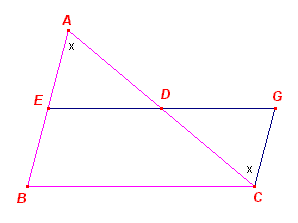In driehoek ABC zijn D en E de middens van AB en AC.
Trek nu CG // AB en verleng ED tot G.
Nu is in de driehoeken ADE, CDG:
(1) A = C (Z-hoeken)
(2) AD = CD
(3) D = D (overstaande hoeken)
Dus ADE, CDG zijn congruent (HZH), waaruit volgt dat CG = AE = EB ......(4)
en
ED = DG = ½EG ......(5)
Nu is BCGE een parallellogram, waaruit volgt dat EG // BC, en dus ook ED // BC.
Maar ook BC = EG, zodat uit (5) volgt: ED = ½BC ¨

2. Twee bewijzen met behulp van een middenparallel

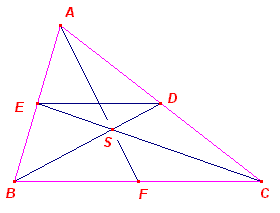Eerste bewijs

In driehoek ABC zijn BD en CE zwaartelijnen.
Nu is DE // BC en DE = ½BC (zie Hulpstelling).
Ook:
SDE, SBC zijn gelijkvormig (hh), waaruit volgt dat BS : DS = BC : DE = 2 : 1
Indien een zwaartelijn een andere zwaartelijn snijdt in een punt S, dan verdeelt dat punt S die zwaartelijn in stukken die zich verhouden als 2 : 1.
Ook de zwaartelijn AF snijdt BD. De ingesneden verhouding op BD is dus eveneens 2 : 1, waaruit volgt dat ook AF door S gaat. ¨

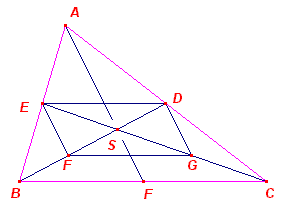Tweede bewijs

D en E zijn weer de middens van AC en AB.
F en G zijn verder de middens van BS en CS.
Nu is DEFG een parallellogram (zie Hulpstelling)
Het punt S is het snijpunt van de diagonalen; maw. FS = SD en dus BF = FS = SD.
Het punt S deelt de zwaartelijn BD is stukken die zicht verhouden als 2 : 1.
Twee zwaartelijnen delen elkaar in stukken met een verhouding 2 : 1. De derde zwaartelijn moet dus ook door hun snijpunt gaan. ¨

3. Direct bewijs

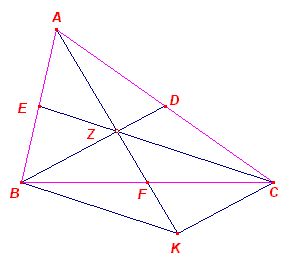In driehoek ABC zijn BD en CE zwaartelijnen. De lijn AZ snijdt BC in F.
We zullen nu aantonen, dat BF = FC.

Verleng AZ met ZK = AZ.
In driehoek AKC is ZD dan middenparallel, zodat ZD // KC en ZD = ½BC.
Gevolg:
BZ // KC en BZ = KC.
BZCK is dan een parallellogram, waarin F het snijpunt is van de diagonalen.
Dus
BF = FC. ¨

4. Bewijs met oppervlaktes

Hulpstelling
De afstanden van twee hoekpunten tot de zwaartelijn van de door die hoekpunten begrense zijde zijn gelijk

Bewijs:

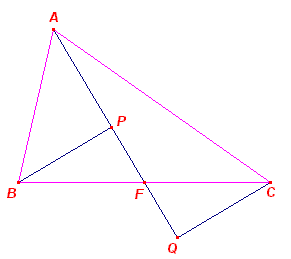In driehoek ABC is AF zwaartelijn, P, Q zijn de voetpunten van bedoelde afstanden.

Nu is:
BPF, CGF zijn congruent (ZHH), waaruit direct volgt dat BP = CQ
¨

We beschouwen nu de zwaartelijn AF als de meetkundige plaats van de punt X waarvoor de oppervlaktes van dr driehoeken XAB, XAC gelijk zijn.

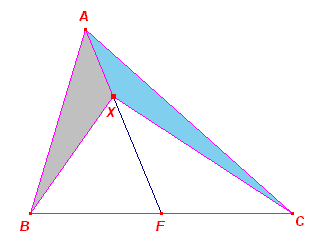Dat deze oppervlaktes inderdaad gelijk zijn volgt uit de hierbovenstaande Hulpstelling; immers beide driehoeken hebben gelijke hoogte en dezelfde basis, te weten AX.
Omgekeerd.
Stel de beide driehoeken hebben dezelfde oppervlakte. Dan is ook de afstand van B tot AF gelijk aan de afstand van C tot AF.
Op grond van de congruentie van BPF en CGF (ZHH), volgt dan dat F het midden is van BC.

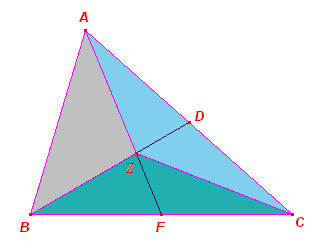Snijden we nu de zwaartelijn AF met de zwaartelijn BD, dan geldt op basis van bovenstaande eigenschap:
   O(ZAB) = O(ZAC), omdat Z op AF ligt; en
   O(ZAB) = O(ZBC), omdat Z op BD ligt.
Gevolg:
   O(ZAC) = O(ZBC)
waaruit volgt dat Z ook ligt op de zwaartelijn door C.

Omdat O(ZBF) = ½O(ZBC) = ½O(ZAB), is
AZ = 2ZF
(immers de driehoeken ZAB, ZBF hebben dezelfde hoogte.
Met andere woorden:
AZ : ZF = 2 : 1

¨
Opmerking
Op grond van continuïteitsoverwegingen kan ook via het gebruikte punt X op AF al besloten worden tot een en ander.
Immers voor X op AF geldt: O(XAB) = O(XAC).
Valt X met A samen dan zijn die oppervlaktes gelijk aan 0. Valt X met F samen dan zijn die oppervlaktes elk gelijk aan de helft van de oppervlakte van driehoek ABC.
Er is dus een punt X = Z op AF waarvoor die oppervlaktes gelijk zijn aan ¹/₃·O(ABC).
Klik hier >< voor een CabriJavapplet die deze opmerking illustreert.
[einde Opmerking]

[zwaartelijn.htm] laatste wijziging op: 02-06-03