Statistiek

Centrummaten | Boxplot | Frequentiepolygoon | Pascal | Literatuur ][ DK & Wiskunde

1. Centrummaten en spreiding
Statistiek is een tak van de wiskunde die zich bezig houdt met het onderzoeken van verschijnselen (gebeurtenissen) in of bij een (grote) groep mensen of objecten.
De te onderzoeken verzameling objecten heet populatie.
Het verzamelen van de gegevens voor het onderzoek wordt gedaan via waarnemingen (tellingen) of enquêtes. Daarbij wordt vaak slechts een klein gedeelte van de populatie onderzocht. Zo'n deelverzameling heet dan steekproef. De resultaten van de onderzochte elementen in de steekproef worden vaak "vertaald" (van toepassing verklaard op) naar de gehele populatie.

Voorbeeld
Een groep van 100 leerlingen (de populatie) heeft een meerkeuze-toets (met 4 alternatieven per vraag) in een bepaald vak afgelegd. Daarbij wordt het aantal goede antwoorden (de toets bestond uit 50 vragen) ingedeeld in klassen van vijf punten.

In figuur 1 een frequentietabel van de resultaten. In figuur 2 staat een staafdiagram van de frequenties.

figuur 1

klasse	f_i	m_i
1-5	0	3
6-10	1	8
11-15	2	13
16-20	5	18
21-25	10	23
26-30	18	28
31-35	25	33
36-40	22	38
41-45	14	43
46-50	3	48

figuur 2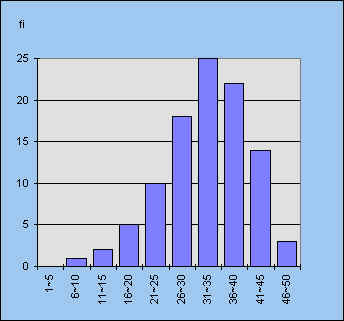

Opmerking
In figuur 1 staat f_i voor de frequentie van de waarnemingen in de bijbehorende klasse en m_i voor het klassenmidden van die klassen. De i kan in dit geval het beste worden gelezen als "individueel". De index is afkomstig uit de schrijfwijze met het sommatieteken (zie de formule voor het gemiddelde, hieronder).
[einde opmerking]

Als maten voor het centrum kennen we

modus (bij klassen: modale klasse)	de waarneming met de hoogste frequentie; in dit geval is dat klasse 41-45
mediaan	de middelste waarneming; in dit geval ligt deze in de klasse 31-35 en is gelijk aan 33 (het midden van de klasse)
gemiddelde	rekenkundig gemiddelde, op deze pagina aangegeven met x^{^_}

Voor het (rekenkundig) gemiddelde geldt (met x_i = waarde van de waarneming; in dit geval de score, en f_i de daarbij behorende frequentie. n is het aantal waarnemingen):

Deze formule kan hier niet direct gebruikt worden omdat de waarden van de waarnemingen (de echte scores) niet hier niet bekend zijn.
In dit geval kiezen we daarvoor de klassenmiddens (m_i). Voor bijvoorbeeld de 2e klasse is dat m₂ = (6 + 10)/2 = 8.
Volgens bovenstaande formule is dan:

Daarbij zij dus opgemerkt, dat dit niet het werkelijk gemiddelde is van de scores, maar het gemiddelde op basis van de keuze van de klassenmiddens.

Voor de zogenoemde spreiding wordt vaak gebruikgemaakt van de standaarddeviatie (ook wel standaardafwijking) die aangegeven wordt met de Griekse (kleine) letter sigma s:
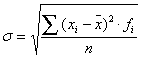
imagesstatis4
De standaardafwijking is dus een "soort" gemiddelde van de absolute afwijkingen tussen de waarnemingsgetallen en het gemiddelde van die waarnemingsgetallen.
Ook hierbij maken we, in geval van klassen, gebruik van de middens van die klassen.
In ons geval geldt (weer op basis van de klassenmiddens): s = 8,13

Opmerking
Een formule voor de standaarddeviatie die gemakkelijker te hanteren is bij berekeningen, luidt:

Te lezen als: het kwadraat van de standaarddeviatie (dat kwadraat wordt ook wel variantie genoemd) is gelijk aan het gemiddelde van de kwadraten van de waarnemingsgetallen verminderd met het kwadraat van het gemiddelde van die getallen.
[einde opmerking]

Statistische vuistregels
De getallen x^{^_}en s worden gebruikt bij het vaststellen van de normering van het examen.
Als een verdeling enigszins lijkt op een zogenoemde normale verdeling dan gelden de volgende vuistregels:

x^{^_} - s en x^{^_} + s zijn grenzen waarbinnen 68% van de waarnemingsgetallen liggen;
x^{^_} - 2s en x^{^_} + 2s zijn grenzen waarbinnen 95% van de waarnemingsgetallen liggen.

Aangezien de gokkans bij een meerkeuze toets met 4 alternatieven gelijk is aan 0,25 per vraag, zal men het cijfer 1 toekennen aan kandidaten, die (in het voorbeeld) 13 of minder goede antwoorden hebben.
In dit geval is x^{^_} - s = 32,7 - 8,13 = 24,57 en x^{^_} + s = 32,7 + 8,13 = 40,83. De betekenis hiervan is dat 68% van de leerlingen een score hebben van 25, 26, ..., 40 goede antwoorden.
Wil men dat 68% van de kandidaten het cijfer 6 hebben of hoger, dan bepaalt men de grens op x^{^_} - 0,45s » 26 goede antwoorden (de factor 0,45 kan worden berekend met behulp van de normale verdeling).

Handmatige berekening
Hieronder (in figuur 3) zetten we bovenstaande berekeningen samen met nog wat andere waarden die bij dit probleem een rol (kunnen) spelen, in een tabel. Een dergelijke tabel is handig als de berekeningen handmatig moeten worden uitgevoerd.
Hierin is:

m_i - het klassenmidden van de bedoelde klasse (in de tabel verder aangeduid als x_i).
rel_f_i - de relatieve frequentie van de meetwaarde (dus f_i / n)
C(f_i) - de cumulatieve frequentie van de meetwaarden
C(rel_f_i) - de cumulatieve relatieve frequentie van de meetwaarden
x²- het kwadraat van het gemiddelde van de meetwaarden (dus x^{^_ .} x^{^_}); deze waarde wordt gebruikt bij de berekening van de standaarddeviatie.(zie de Opmerking hierboven in paragraaf 1)

figuur 3

klasse	f_i	m_i = x_i	x_i ^. f_i	rel_f_i	C( f_i )	C(rel_f_i)	x_i²	x_i² ^. f_i	x²
1-5	0	3	0	0	0	0	9	0
6-10	1	8	8	0,01	1	0,01	64	64
11-15	2	13	26	0,02	3	0,03	169	338
16-20	5	18	90	0,05	8	0,08	324	1620
21-25	10	23	230	0,1	18	0,18	529	5290
26-30	18	28	504	0,18	36	0,36	784	14112
31-35	25	33	825	0,25	61	0,61	1089	27225
36-40	22	38	836	0,22	83	0,83	1444	31768
41-45	14	43	602	0,14	97	0,97	1849	25886
46-50	3	48	144	0,03	100	1	2304	6912
totalen	100		3265					113215	1066,023
gemiddelden			32,65					1132,15
standaarddeviatie			8,131882

2. Boxplot
Bij het gebruik van de mediaan worden eveneens spreidingsgetallen gebruikt.
Bij een geordende eindige waardenverzameling met een oneven aantal elementen is de mediaan gelijk aan het middelste getal.
Is het aantal elementen even, dan is de mediaan het gemiddelde van de beide "middelste" getallen.
Links en rechts van de mediaan van zo'n verzameling ligt dus steeds 50% van de waarnemingen.
De mediaan van het linker deel van de waardenverzameling heet 1e kwartiel; de mediaan van het rechter deel van de verzameling heet 3e kwartiel (de mediaan zelf wordt soms 2e kwartiel genoemd.
Het verschil tussen het 3e kwartiel en het 1e kwartiel heet kwartiele afstand of kwartiele variatie.
Deze vier gegevens kunnen grafisch worden weergegeven in een bijzondere grafiek, de zogenoemde boxplot van de gegevens. In figuur 4 is dat gedaan voor de middens van de klassen uit het in paragraaf 1 genoemde voorbeeld.

figuur 4

1e kwartiel = 28
mediaan = 33
3e kwartiel = 38
1,5 maal kwartiele afstand = 1,5 ^. 10 = 15
33-15=18; 33+15=48

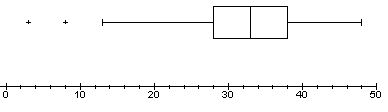De boxplot bestaat dus (in het algemeen) uit twee gedeelten: een getallenlijn en een figuur (de "plot") waarmee de kwartielen en de mediaan worden aangegeven. De plot zelf bestaat uit

een "centraal" lijnstuk dat de mediaan aangeeft;
twee lijnstukken die de beide kwartielen aangeven;
twee kleine lijnstukken op een afstand van maximaal 1,5 maal de kwartiele afstand (niet verder dan de grootste cq. de kleinste meetwaarde);
punten die buiten het bereik van 1, 5 maal de kwartiele afstand liggen.

3. Frequentiepolygoon
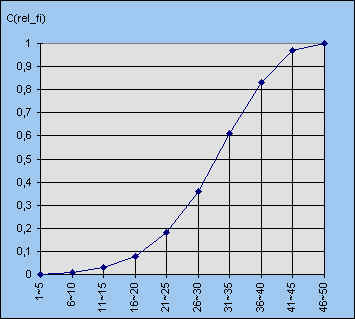
Op basis van de in figuur 3 staande berekening kunnen we ook een histogram maken van de cumulatieve (relatieve) frequenties. In figuur 5 hebben we de balken van het histogram aan elkaar laten aanluiten. Wanneer we nu de rechter eindpunten van de rechthoeken met elkaar verbinden, krijgen we een zogenoemd frequentiepolygoon, behorende bij de cumulatieve relatieve frequenties (zie figuur 6).

figuur 5	figuur 6

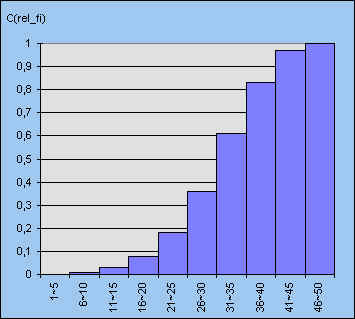Opmerking
In figuur 6 is van de klasse 1-5 alleen het rechter eindpunt in de figuur opgenomen!
De verticale lijnen geven het eindpunt van de klasse aan.
[einde opmerking]

We kunnen van figuur 6 gebruik maken om, via de 25%, 50% en de 75% lijn, het 1e kwartiel, de mediaan en het 3e kwartiel af te lezen op de horizontale as.

4. Systematisch tellen, de driehoek van Pascal
Bij statistisch onderzoek wordt geteld. Vaak komt het voor dat van een aantal elementen in een populatie (of steekproef) niet meer behoeft te worden gedaan, dan het tellen van het aantal rangschikkingen.
We bekijken opvolgend het aantal rangschikkingen van een populatie met 1, 2 en 3 elementen (zie figuur 6).

figuur 6
poulatie	{A}	{A, B}	{A,B,C}
rangschikkingen:	A	AB BA	ABC BCA CAB ACB CBA BAC
aantal	1	2	6

Wanneer we nu een vierde element (D) erbij betrekken, dan kunnen we, als we alleen de rangschikking ABC bekijken, 4 plaatsen voor D binnen deze rangschikking vinden:
DABC
ADBC
ABDC
ABCD
Het aantal rangschikkingen van een populatie 4 met elementen is dus 6 ^. 4 = 24.

Definities
Het aantal rangschikkingen van een populatie van n elementen schrijven we als n! (spreek uit: "n faculteit").

Wanneer we naar een deelverzameling van een populatie (met n elementen) bekijken en we nemen daar k (met k £ n) elementen uit, dan is het aantal rangschikkingen van deze k elementen gelijk aan n . (n - 1) . (n - 2) ... (n - k + 1) = n! / (n - k)!
Dit aantal geven we soms aan met nPk.

Wanneer we in deze laatste rangschikkingen de ordening buiten beschuouwing laten, dan vinden we het aantal verschillende manieren waarop we uit n elementen er k kunnen kiezen.
Dit aantal kunnen we vinden door nPk te delen door het aantal permuaties van de k (nu ongeordende) elementen.
We schijven dit aantal vaak als
of als nCk, en noemen dat het aantal combinaties van k uit n elementen.

We zien dus dat n! = (n - 1)! ^. n

De getallen nCk heten ook wel binomiaalcoëfficiënten.

Gevolg
Nemen we k = n, dan is nPn = n!, zodat (n - n)! = 0! = 1,

Voor waarden van n = 0, 1, ... , 12 en k = 0, 1, ..., n staan de binomiaalcoëfficiënten in figuur 7. Deze figuur wordt ook wel de Driehoek van Pascal genoemd.

figuur 7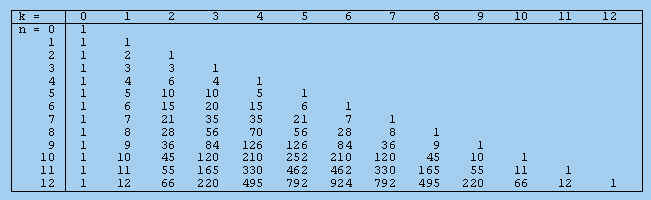

De binomiaalcoëfficiënten worden (oa.) gebruikt bij de binomiale kansverdeling.

Literatuur

[1] Zie bijvoorbeeld het boekje EHBS - www.hulpbijstatistiek.nl (tbv. TI83 grafische rekenmachine)
[2] Zie ook TI83 werkbladen.

[statistiek.htm] laatste wijziging op: 13-10-2003