Kansrekening
1. Definitie van het begrip kans,
kansregels
Experimenten, waarvan wordt geŽist dat ze een onbeperkt aantal keren kunnen worden
herhaald onder gelijkblijvende omstandigheden, worden kansexperimenten genoemd.
De verzameling van alle mogelijk uitkomsten van zo'n kansexperiment heet de uitkomstenruimte
U.
Onder een gebeurtenis A verstaan we een deelverzameling van U.
| Definitie In deze definitie gaan we uit van een eindige uitkomstenverzameling, waarbij de uitkomsten even waarschijnlijk zijn. Onder de kans op gebeurtenis A Ő U, notatie P(A), verstaat men het quotiŽnt van het aantal voor A gunstige uitkomsten en het aantal mogelijke uitkomsten. Dus (definitie van Laplace) 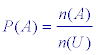 De onmogelijke gebeurtenis heeft kans 0; de zekere gebeurtenis heeft kans P(U) = 1. |
We zullen aan de hand van een voorbeeld de kansdefinitie wat verder toelichten.
Voorbeeld
Men werpt ťťn keer met een groene (in figuur 1 aangegeven met de
letter G) en een zwarte (zie de letter Z in figuur 1) zuivere
dobbelsteen. Of er na elkaar of tegelijkertijd met die dobbelstenen wordt geworpen, laten
we in het midden, omdat we uitsluitend geÔnteresseerd zijn in de volgende uitkomst van
het experiment "de som van het aantal ogen".
De uitkomstenruimte bestaat uit alle paren (G, Z),
waarbij G = 1, 2, ... ,6 en Z = 1, 2, ..., 6.
Nu is dus n(U)=36.
We kunnen deze uitkomsten weergeven als punten in een zogenoemde matrix (zie figuur 1).
| figuur 1 | 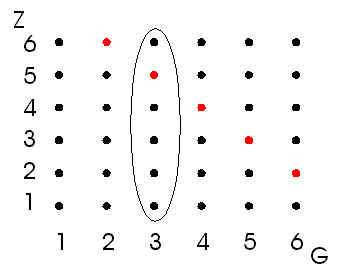 |
Merk op, dat bijvoorbeeld de worp (2,6) een andere uitkomst is dan (6,2)!
Denk daarbij aan de kleur van de dobbelstenen. We beschouwen nu de volgende gebeurtenis
A: "de som van het aantal ogen is gelijk aan 8." Uit de matrix volgt dus dat P(A) = 5/36. |
Beschouwen we de gebeurtenis B: "de groene (G) dobbelsteen heeft 3 ogen" (het
aantal ogen op de zwarte steen is dus niet interessant).
Nu is P(B) = 6/36 (zie de 6 omlijnde punten).
We kunnen nu de gebeurtenis C: "de som van de aantallen ogen is 8 EN
(tegelijkertijd) het aantal ogen op de groene steen is gelijk aan 3" bekijken.
De gebeurtenis C is samengesteld uit de gebeurtenissen A en B door het gebruik van het
woord EN. We schijven:
C = A « B (spreek uit: "A en tegelijkertijd
B").
Zodat P(C) = P(A « B) = 1/36 (zie de rode punt in het omlijnde
gebied).
We kunnen ook de volgende gebeurtenis beschouwen, D: "de som van het aantal ogen
is gelijk aan 8 OF de groene dobbelsteen heeft 3 ogen".
De gebeurtenis D is samengesteld uit de gebeurtenissen A en B door het gebruik van het
woord OF. We schrijven: D = A » B (spreek uit "D is
gelijk aan A of B").
Nu is:
P(D) = P(A » B) = P(A) + P(B) - P(A « B)
immers bij het optellen van de P(A) en P(B) tellen we het rode, omlijnde punt dubbel;
zodat
P(A » B) = 5/36+6/36-1/36=10/36
Als geldt, dat P(A) + P(B) = P(A » B), dan noemen we A en B
"elkaar uitsluitende gebeurtenissen". In dit geval hebben de beide
"verzamelingen" punten in de matrix dus geen enkel punt gemeenschappelijk.
Dus:
- Algemeen: P(A » B) = P(A) + P(B) - P(A « B) ; dit wordt de somregel genoemd.
- Bij elkaar uitsluitende gebeurtenissen: P(A » B) = P(A) + P(B)
Iedere gebeurtenis A heeft in U een zogenoemd complement. Het complement van A
wordt uit A afgeleid door het gebruik van het woord NIET. Dus is in bovenstaand voorbeeld
het complement van A de gebeurtenis "de som van het aantal ogen is NIET 8".
Schrijfwijze: ōA (spreek uit: "niet A").
We zien dat in het voorbeeld P(ōA) = (36-5)/36 = 31/36.
Dus
- Algemeen: P(ōA) = 1 - P(A) of ook P(A) + P(ōA) = 1 ; dit wordt de complementsregel of ontkenningsregel genoemd.
2. Voorwaardelijke kans, onafhankelijke kansen
| Definitie Onder de "voorwaardelijke kans op gebeurtenis A gegeven gebeurtenis B" verstaan we de kans, dat A optreedt, terwijl we "van te voren" de eis stellen, dat de gebeurtenis B optreedt. Notatie: P(A|B) (spreek uit: "de kans op A onder de voorwaarde B" of "de voorwaardelijke kans op A, gegeven B"). In plaats van de uitkomstenruimte U kiezen bij een dergelijk experiment de uitkomstenruimte B. Zodat per definitie geldt: 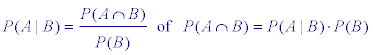 |
Voorbeeld
Experiment: ťťnmaal gooien met twee dobbelstenen (een zwarte en een groene)
gebeurtenis A: "het aantal van de ogen is 8"
gebeurtenis B: "op de groene 5 of 6 ogen"
Nu is P(A|B) = 2/12 en P(B|A) = 2/5.
| Definitie Twee gebeurtenissen heten onafhankelijk, als P(A « B) = P(A) . P(B) |
Voorbeeld
Experiment: men werpt een dubbeltje en een gulden.
gebeurtenis Kd: "het dubbeltje is kop"; gebeurtenis Mg:
"de gulden is munt"
Nu is: P(Kd « Mg) = 1/4, P(Kd)
= 1/2 en P(Mg) = 1/2. De gebeurtenissen Kd en Mg zijn dus
onafkankelijk.
Dat beide gebeurtenissen onafhankelijk zijn volgt natuurlijk ook direct uit de opbouw van
het experiment.
Het kan voorkomen, dat gebeurtenissen die niet "los van elkaar staan" toch onafhankelijk zijn. Het begrip onafhankelijk heeft in de wiskunde dus een duidelijk andere betekenis, dan in het dagelijks gebruik.
Voorbeeld
In een vaas zitten 6 gekleurde en genummerde ballen. De ballen 1 en 4 zijn wit (W); de
ballen 2, 3, 5 en 6 zijn rood (R).
Experiment: we trekken ťťn bal ui de vaas en beschouwen de volgende gebeurtenissen:
O: "de trekking is oneven"
E: "de trekking is even"
R: "de trekking is een rode bal"
De gebeurtenissen O en R zijn nu onafhangelijk De gebeurtenissen E en R trouwens ook.
| P(O) = 3/6 P(E) = 3/6 P(R) = 4/6 |
P(O « R) = 2/6 P(E « R) = 2/6 |
In beide gevallen is immers 2/6 = 3/6 . 4/6. |
| Definitie Een stochastische variabele of stochast is een functie X die de elementen van de uitkomstenruimte afbeeldt op de reŽle getallen. Zij dus U = {u1, u2, u3, ..., un} dan is X(u i ) met i = 1, 2, ..., n de bedoelde stochast. De stochast wordt meestal alleen aangeduid met de letter X. Voor de waarden van de stochast X wordt dan de letter x (of k) gebruikt. Onder een kansverdeling verstaat men functie P(X = x). |
Toelichting
In een vaas bevinden zich 3 rode knikkers en 7 witte.
Experiment: er wordt 4 maal een knikker uit de vaas getrokken en het resultaat genoteerd;
na het trekken wordt de knikker weer in de vaas gedaan (trekking met
teruglegging).
De stochast X wordt nu gedefinieerd als het totaal aantal getrokken rode knikkers We
schrijven wel:
X = aantal rode knikkers.
Nu is U = {0, 1, 2, 3, 4}
| P(X = 0) | = | 1 x 7/10 x 7/10 x 7/10 x 7/10 = 1 x (0,3)0(0,7)4 = 0,2401 |
uitkomst: | WWWW |
| P(X = 1) | = | 4 x 3/10 x 7/10 x 7/10 x 7/10 = 4 x (0,3)1(0,7)3 = 0,4116 | RWWW of WRWW of WWRW of WWWR | |
| P(X = 2) | = | 6 x 3/10 x 3/10 x 7/10 x 7/10 = 6 x (0,3)2(0,7)2 = 0,2646 | RRWW of RWRW of RWWR of WRRW of ... | |
| P(X = 3) | = | 4 x 3/10 x 3/10 x 3/10 x 7/10 = 4 x (0,3)3(0,7)1 = 0,0756 | RRRW of RRWR of RWRR of WRRR | |
| P(X = 4) | = | 1 x 3/10 x 3/10 x 3/10 x 3/10 = 1 x (0,3)4(0,7)0 = 0,0081 | RRRR |
We schrijven de kansverdeling vaak horizontaal, dus:
| x | 0 | 1 | 2 | 3 | 4 | |
| P(X = x) | 0,2401 | 0,4116 | 0,2646 | 0,0756 | 0,0081 | Merk hierbij op, dat de som van deze kansen gelijk is aan 1. |
Onafhankelijke stochasten en simultane verdeling van stochasten
| Definities Twee stochasten X en Y heten onafhankelijk als voor alle x en y geldt P(X = x Ŕ Y = y) = P(X = x) . P(Y = y) Beschouwen we twee of meer verschillende stochasten, dan noemen we de daarbij behorende kansverdeling een simultane kansverdeling. |
Voorbeeld
Experiment: werpen met twee dobbelstenen.
X = "som van het aantal ogen"; Y = "(absolute) verschil van het aantal
ogen"
De simultane kansverdeling van X en Y is in de volgende tabel (zie figuur 2) weergeven.
| figuur 2 |
 |
Uit deze verdeling is duidelijk, dat er geen sprake is van onafhankelijkheid van X en Y, immers (bijvoorbeeld)
P(X = 2 en Y = 0) = 1/36, terwijl P(X = 2) . P(Y = 0) = 1/36 . 6/36.
4. Binomiale verdeling
Een herhaald kansexperiment waarbij slechts twee uitkomsten mogelijk zijn (bij
aselecte en onafhankelijke trekkingen, met teruglegging), wordt een binomiaal
kansexperiment (ook wel kortweg alternatief) genoemd.
Vaak worden de uitkomsten aangeduid als "succes" (S) of "mislukking"
(M).
De kans op succes wordt dan aangeduid met p.
De getallen n en p heten de parameters van de binomiale
stochast.
Bij n herhalingen van het experiment wordt de kansverdeling van X gegeven door
![]()
Deze verdeling heet de binomiale verdeling; notatie B(n, p)
of ook wel Bin(n, p). In de formule heten
de factoren van de vorm ![]() binominaalcoŽfficiŽnten. Zo'n getal wordt ook wel aangegeven met nCk;
je ziet soms ook wel (n)k.
binominaalcoŽfficiŽnten. Zo'n getal wordt ook wel aangegeven met nCk;
je ziet soms ook wel (n)k.
Toelichting
In de toelichting in paragraaf 3 hebben we gebruik gemaakt van de
binomiale verdelingen voor n = 4 en p = 0,3.
We kunnen met de gegevens uit die toelichting ook de zogenoemde cumulatieve binomiale
verdeling opstellen; dwz. we bekijken voor x = 0, 1, 2, 3, 4 de kans P(X £ x). We krijgen dan
| x | 0 | 1 | 2 | 3 | 4 | |
| P(X£x) | 0,2401 | 0,2401 + 0,4116 = 0,6517 |
0,2401 + 0,4116 + 0,2646 = 0,9163 |
0,9163 + 0,0756 = 0,9919 |
0,9919 + 0,0081 = 1 |
Van cumulatieve binomiale verdelingen als deze zijn voor verschillende waarden van n en p tabellen gemaakt. Een deel uit zo'n tabel staat in figuur 3. Bovenstaande waarden zijn daarin, nu weer in een kolom weergegeven, terug te vinden.
| figuur 3 |
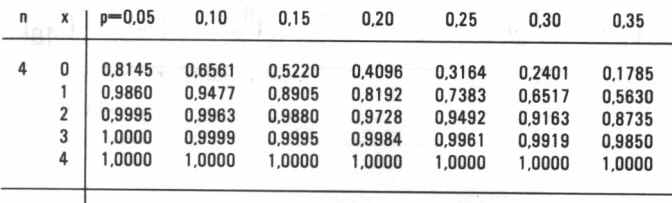 |
Gevolg
Bij gebruik van dit type tabellen kan de kans P(X = k) als volgt gevonden worden
P(X = k) = P(X £ k) - P(X £
k - 1)
Zo is P(X = 2 | n = 4, p = 0,15) = P(X £ 2) - P(X £ 1) = 0,9880 - 0,8905 =
0,0975 (zie figuur 2)
Deze kans kunnen we natuurlijk ook met de definitie berekenen:
P(X = 2) = (4C2) (0,15)2(0,85)2 = 0,0975
De kansverdeling van een binomiale stochast kan met een staafdiagram in beeld worden gebracht.
| figuur 4 - n = 6 | figuur 5 - n = 20 |
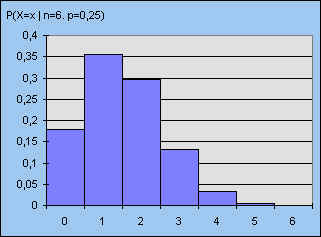 |
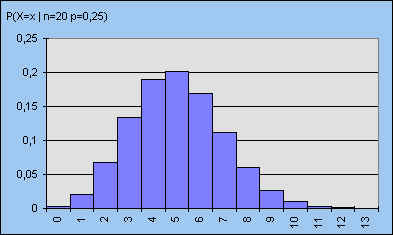 |
We zien bij vergelijking van beide verdelingen, dat bij grotere waarden van n de symmetrie van de verdeling toeneemt, waarbij tevens de vorm van de verdeling de zogenoemde klokkromme (behorend bij de normale verdeling) benadert.
Ter illustratie van dit laatste staat in figuur 6 nog een derde verdeling met kans p = 0,25.
| figuur 6 - n = 50 |
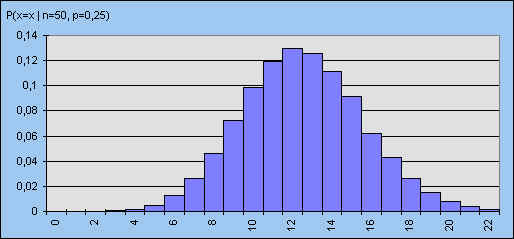 |
Door deze eigenschap is het mogelijk de binomiale verdeling in sommige gevallen te benaderen met behulp van de normale verdeling.
5. Karakteristieken: verwachting, variantie en standaarddeviatie
| Definities Zij X een stochast gedefinieerd op een uitkomstenverzameling U = {x1, x2, ..., xn} met kansverdeling P(X = xi), dan is de verwachting van X of verwachtingswaarde van X het getal Hierbij is dus n het aantal elementen in de uitkomstenverzameling. We schrijven soms voor de duidelijkheid ook E[X] in plaats van E(X). Onder de variantie van
een stochast X verstaan we het getal Var[X] = E[(X - m)2],
waarbij m = E[X]. |
Voorbeeld
Voor n = 4 en p = 0,3 hebben we dus (zie voor de kansen de Toelichting
in paragraaf 3):
E[X] = 0 x 0,2401 + 1 x 0,4116 + 2 x 0,2646 + 3 x 0.0756 + 4 x
0,0081 = 1,2000
Var[X] = (0-1,2)2 x 0,2401 + (1-1,2)2 x 0,4116 + (2-1,2)2 x 0,2646 + (3-1,2)2 x 0,0756 + (4-1,2)2 x 0,0081 =
0,8400
s[X] = (0,8400)1/2 = 0,9165
We kunnen de volgende stelling voor Var[X] bewijzen (de daarin genoemde eigenschap is eenvoudiger te gebruiken dan de definitie):
Stelling 5.1
Var[X] = E[X2] - E[X]2
Dus, doorgaande op het laatste voorbeeld,
E[X2] = 0 x 0,2401 + 1 x
0,4116 + 4 x 0,2646 + 9 x 0,0756 + 16 x 0,0081 = 2,28; en dus
Var[X] = 2,28 - (1,2)2 = 0,8400
Voor het bewijs van stelling 1 verwijzen we naar het gevolg van stelling 7.
Stelling 5.2
Is X een stochast en zijn a en b constanten, dan geldt E[aX + b] = a .
E[X] + b
Bewijs: Volgens de definitie is E[aX + b] = S (axi + b) .
P(X = xi) , waarbij de som S wordt genomen over i
= 1, 2, ..., n. Dus
E[aX + b] = S [ axi .
P(X = xi) + b . P(X = xi) ] =
a . S xi .
P(X = xi) + b . S
P(X = xi) =
a . E[X] + b . 1
®
Stelling 5.3
Voor afhankelijke en onafhankelijke stochasten X en
Y geldt E[X + Y] = E[X] + E[Y]
Bewijs: Volgens de definitie van verwachting moet er worden gesommeerd over
alle uitkomsten. Als n(UX) = m en n(UY) = n, dan
is het aantal uitkomsten van X+Y gelijk aan mn. Dus
E[X + Y] = S { X(ui) + Y(ui) } .
P(ui) = S X(ui) .
P(ui) + S Y(ui) .
P(ui) = E[X] + E[Y]. ®
Gevolg
We kunnen stelling 3 gemakkelijk uitbreiden tot een een stelling voor een som van meer dan
twee stochasten:
E[ X1 + X2 + ... + Xn ] = E[X1] + E[X2] + ... + E[Xn]
Stelling 5.4
Voor onafhankelijke stochasten X en Y geldt E[X .
Y] = E[X] . E[Y]
Bewijs: Als n(UX) = m en n(UY) = n,
dan is
E[X . Y] = Si=1..m
Sj=1..n xiyj P(xi,
yi) = (vanwege de onafhankelijkheid van X en Y)
= Si=1..m Sj=1..n
xiyj P(Xi) P(Yj)
= Si=1..m { xi P(xi) Sj=1..n yj P(yj) }
= Si=1..m { xi P(xi) E[Y] }
= E[Y] Si=1..m xi P(xi)
= E[Y] E[X] ®
Stelling 5.5
Voor een binomiaal verdeelde stochast X met parameters n en p geldt E[X] = n .
p
Bewijs: De binomiale stochast X is het totaal aantal successen in de reeks van
n experimenten met elke een kans p. We definiŽren nu voor i =
1, 2, ..., n
Xi = 1, als het i-de experiment een succes oplevert
Xi = 0 bij een mislukking in het i-de experiment.
Dan is
X = X1 + X2 + ... + Xn.
Voor elke i = 1, 2, ..., n is nu
E(Xi] = 0 . (1 - p) + 1 .
p = p
Blijkens het gevolg bij stelling 3 hebben we dan E[X] = E[X1] + ... + E[Xn]
= n . p ®
Stelling 5.6
Var[aX + b] = a2 Var[X]
s{aX + b] = | a | s[X]
Bewijs: Var[X] = Si=1..n (axi
+ b - E[aX + b])2 . P(X=xi)
= S i=1..n (axi + b - a
E[X] - b)2 P(X=xi)
= a2 S i=1..n (xi -
E[X])2 P(X=xi)
= a2 Var[X]
Het tweede deel van de stelling volgt hieruit door worteltrekking. ®
Stelling 5.7
Zij c een constante, en is m = E[X], dan is Var[X] = E[
(X-c)2 ] - (m -c)2
Bewijs: Var[X] = E[ (X-m)2 ] = E[ (X - c) - (m - c)2 ]
= E[ (X - c)2 ]- 2(X - c)(m - c) + (m - c)2 ] = E[ (X - c)2 ] - 2(m-c)E[X - c]
+ (m-c)2
= E[ (X - c)2 - 2(m-c)(m-c)
+ (m-c)2 = E[ (X - c)2 ] - (m -
c)2 ®
Gevolg
Is c = 0 dan vinden we Var[X] = E[ X2 ] - m2 (zie stelling 1).
Stelling 5.8
Zijn X en Y onafhankelijke stochasten, dan is
Var[X + Y] = Var[X] + Var[Y] OF s[X + Y] =
( s{X]2 + s[Y]2
)1/2
Bewijs: Var{X+Y] = volgens stelling 7
= E[ (X+Y)2 ] - (E[ X+Y])2 = E[ X2 +2XY + Y2 ]
- (E[X] + E[Y])2
= E[X2] +2E[XY] + E[Y2] - (E[X])2 - 2 E[X]E[Y] - (E[Y])2
= E[X2] - (E[X])2 + E[Y2] -
(E[Y])2 = weer volgens stelling 7
= Var[X] + Var [Y] ®
Gevolg
Stelling 8 is eenvoudig uit te breiden tot
Stelling 5.8*
Zijn X1, X2, ..., Xn onderling onafhankelijke
stochasten, dan is
Var[X1 + X2 + ... + Xn] = Var[X1]
+ Var[X2] + ... + Var[Xn]
| Stelling 5.9 | |
| Een binomiale stochast X met parameters n en p heeft een standaardafwijking |
Bewijs: Er wordt n keer onafhankleijk een experiment herhaald met kans p
op succes en kans (1-p) mislukking. We definiŽren nu voor i = 1, 2,
..., n
Xi = 1, als het i-de experiment een succes oplevert
Xi = 0 bij een mislukking in het i-de experiment (zie ook
stelling 5)
Dus P(Xi = 1) = p en P(Xi = 0) = 1 - p
Var[Xi] = E[ Xi2] - (E[Xi])2 = { 02
x (1 - p) + 12 x p
} - ( 0 x (1 - p) + 1 x p)2
= p - p2 = p(1 - p).
Toepassing van stelling 5.8' geeft nu
Var[X] = Var[X1 + X2 + ... +Xn] = Var[X1} +
... Var[Xn] = np(1 - p). ®
6. Normale verdeling
Naast discrete kansverdelingen zijn er ook continue. Het is daarbij niet meer mogelijk de
kansen op afzonderlijke waarden waarden van X aan te geven, want voor elke waarde is
die kans gelijk aan 0.
Wel kan de kans op hele intervallen van waarden worden vastgelegd.. Dit gebeurt door een kansdichtheidsfunctie
f(x).
Voor zo'n stochast X is de kans om een waarde in het interval [a ; b] te vinden
gelijk aan:
![]()
dus juist de oppervlakte onder de grafiek van de functie f(x) op
het interval [a ; b].
Een continue kansverdeling wordt dus vastgelegd door een kansdichtheid f(x),
een niet-negatieve functie met totale integraal 1.
|
|||||||||
Uit de definitie van de deze verdeling moge duidelijk zijn, dat de kansen zelf niet eenvoudig te berekenen zijn. Vandaar dat men voor de standaardnormale verdeling een tabel heeft opgesteld (zie figuur 7 voor een gedeelte van zo'n tabel).
| figuur 7 - Cumulatieve normale verdelingsfunctie F(z) = P(Z £ z) | |
 |
De waarden in deze tabel zijn cumulatief naar de speciale stochast Z.
De waarden z van Z staan in de tabel in twee decimalen.
De eerste decimaal staat verticaal links, de tweede decimaal staat horizontaal bovenaan.
Voorbeeld
F(0,23) = P(Z £
0,23) = 0,5910
In figuur 8 staat de grafiek (de klokkromme of kromme van Gauss) van de standaardnormale verdeling
| figuur 8 | |
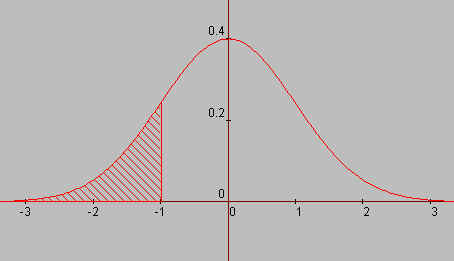 |
Hiernaast is het gebied waarvoor P(Z £ -1)
gearceerd. In de tabel zien we dat F(1) = 0.8413. Dus F(-1) = 1 - F(1) = 1 - 0,8413 = 0, 1587. Hieruit vinden we dus eenvoudig |
[einde voorbeeld]
Elke normale verdeling kan via een zogenoemde schaal- en plaatstransformatie
teruggebracht worden tot de standaardnormale verdeling. Daarom kan de F-tabel
gebruikt worden bij alle normale verdelingen. Het uitvoeren van zo'n transformatie heet
ook standaardiseren.
De transformatie wordt uitgevoerd door de verwachting naar de oorsprong te verschuiven en
dan te meten met de standaarddeviatie van die verdeling als eenheid.
Voor de getransformeerde stochast Z geldt dan Z = (X - m)
/ s.
7. Hypergeometrische verdeling
De binomiale verdeling kan worden verkregen bij een kansexperiment waarbij uit een vaas
met n ballen, a rode en b witte, telkens een rode bal wordt getrokken, met
teruglegging.
De stochast X is hier: het aantal rode ballen in de steekproef.
De kans p op een rode bal is gelijk aan a/n; de kans op een witte bal is b/n (met n = a +
b).
Voor de kans op k rode ballen geldt nu bij n trekkingen :
| P(X = k) = | (a/n)k . (b/n)n-k met n = a + b |
Wanneer we echter het bovenstaande experiment zonder teruglegging uitvoeren krijgen een kansverdeling die we de hypergeometrische verdeling noemen.
| Voor een greep van k ballen uit n ballen zijn er | mogelijkheden. Elke kans heeft dus de waarde 1 / |
| Het aantal grepen bestaande uit k rode en n - k witte ballen is gelijk aan |
| Dus is P(X = k) = | 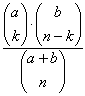 |
Voor de hypergeometrische verdeling zijn er geen tabellen.
8. Centrale limietstelling,
benadering binomiale verdeling
Een stelling die we hier niet bewijzen (maar die we zeker met behulp van voorbeelden
kunnen onderzoeken) luidt
Stelling 8.1 (centrale limietstelling)
De som en het gemiddelde van een (voldoende) groot aantal onafhankelijke stochasten is
(nagenoeg) normaal verdeeld.
Daarbij moeten alle stochasten dezelfde verdeling hebben.
We passen deze stelling (vaak) toe op de binomiale verdeling. Bij zo'n verdeling wordt een totaal geteld (elk succes tellen we als 1, elke mislukking tellen we als 0). Deze binomiale stochast B(n,p) kan daarom worden opgevat als de som van n (onafhankelijke) stochasten.
Volgens de centrale limietstelling geldt dan:
Stelling 8.2
Voor (voldoend) grote waarden van n kan de binomiale stochast B(n,k) met verwachting m = np en standaarddeviatie
Hoe de in de stelling genoemde benadering het beste kan worden berekend zien we in het onderstaande. We geven een
Voorbeeld
Bereken de kans op minder dan 25 keer munt in 70 worpen met een zuiver geldstuk.
We hebben te maken met een biomiaal experiment met n = 70 en p = 0,5.
X = "aantal keer munt".
Tabellen met de binomiale verdeling hebben (meestal) geen kansverdelingen voor n
= 70. We benaderen dus met de normale verdeling.
Nu is m = np = 70 . 0,5
= 35 en s = ÷(70 .
0,5 . (1 - 0,5)) = 4,18.
In figuur 9 zien we hoe de bedoelde benadering tot stand komt. In de figuur links is in
grijs weergegeven de waarde van P(X<=24). Indien we willen benaderen met de normale
verdeling (zie de rode grafiek), dan maken we een fout die ongeveer gelijk is aan de halve
grijze kolom bij 24.
Indien we echter een zogenoemde continuÔteitscorrectie uitvoeren (zie
figuur rechts), dan kunnen we deze fout kleiner maken. De witte vlakjes onder de grafiek
worden dan min of meer gecompenseerd door de grijze vlakjes erboven.
| figuur 9 | 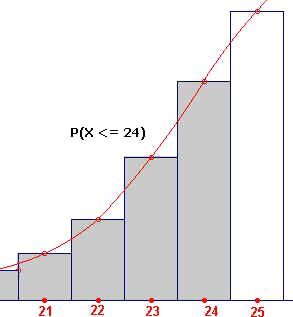 |
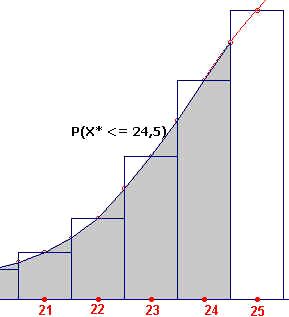 |
Bij benadering is nu P(X £ 24 | n=70, p=0,5) = P(X* <
24,5) waarbij X* een normaal verdeelde stochast is met dezelfde verwachting en
standaardeviatie als X.
Via standaardiseren van X* kan de waarde worden bepaald met gebruikmaking van de
standaardnormale verdeling (via een tabel met waarden van de functie F).
We voeren nu de standaardisatie uit.
P(X £ 24 | n=70, p=0,5) = P(X* < 24,5) = P(Z < (24,5 -
35) / 4,18) = P(Z < -2,51)
In de F-tabel vinden we dat deze kans gelijk is aan 0,0060.
Wanneer we de werkelijke waarde van P(X £ 24 | n=70, p=0,5)
berekenen, vinden we 0,0058.
[einde Voorbeeld]
We hebben dus min of meer de volgende
Stelling 8.3
Als men de binomiale verdeling van een stochast X kan benaderen door een normaal verdeelde
stochast X*, dan geldt
P(X £ b ) = P(X* < b + Ĺ)
P(X ≥ a ) = P(X* > a - Ĺ
P(a £ X £ b) = P(a - Ĺ < X*
< b + Ĺ)
9. De ÷n-wet, som en gemiddelde van onafhankelijke stochasten
Hebben de stochasten X1, X2, ..., Xn betrekking op n
onafhankelijke uitvoeringen van hetzelfde kansexperiment, dan geldt:
E[X1] = E[X2] = ... = E{Xn}.
Het totaal (de som) van de stochasten X1, ..., Xn is zelf ook weer
een stochast T, met als verwachtingswaarde
E[T] = E[X1 + X2 + ...
+ Xn] = n . E[X1].
Verder geldt
Var[T] = Var[X1 + X2 + ...
+ Xn] = n . Var[X1]
en
SD[T] = SD[X1 + X2 + ...
+ Xn] = ÷(n . Var[X1])
= ÷n . SD[X1]
Is men geÔnteresseerd in het gemiddelde van de stochasten X1, X2, ..., Xn,
dan kunnen we ook het gemiddelde opvatten als een stochast G. Hiervoor geldt dan
G = 1/n (X1 + X2 + ...
+ Xn)
Volgens stelling 5.2 is E[cX] = c E[X] en volgens stelling 5.6 geldt Var[cX] = c2 Var[X].
Passen we dit toe op de stochast G, dan vinden we
E[G] = E[1/n . T] = 1/n . E[T]
= 1/n . n . E[X1]
= E[X1]
De variantie van de stochast G is dan
Var[G] = (1/n)2 . Var[T]
= (1/n)2 . n . Var[X1]
= 1/n . Var[X1]
Hieruit volgt dan voor de standaarddeviatie van G
SD[G] = ÷(Var[G]) = ÷(1/n . Var[G])
= 1/÷n . SD[X1]
We hebben nu bewezen
Stelling 9.1
Is bij een experiment een stochast X gedefinieerd, dan geldt bij n onafhankelijke
uitvoeringen van dit experiment, dat de SD van het gemiddelde van de waarden van X ÷n zo klein is als de SD van X zelf.
Deze stelling wordt wel de ÷n-wet of de wet van de afnemende standaarddeviatie genoemd.
10. Cumulatieve grafieken
Van de F-tabel (van de cumulatieve normale verdeling) kan een
grafiek gemaakt worden. Langs de horizontale as staan de waarden van de stochast Z en
langs de verticale as staan de (gecumuleerde) kansen (zie de rode lijn in figuur 10). Deze
grafiek heet de cumulatieve normaalkromme (ook wel standaardnormale
verdelingsfunctie).
De punten P en Q hebben opvolgend de coordinaten (1; 0,84) en (-1; 0,16). De horizontale
lijnen door deze punten zijn dus de 84%- en de 16%-lijn. Voorts is ook de 50%-lijn
getekend.
| figuur 10 | 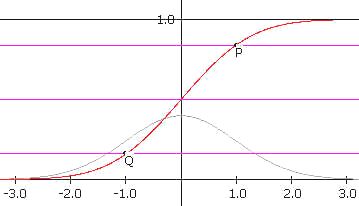 |
Uit de cumulatieve normaalkromme kunnen gemiddelde en standaarddeviatie
worden afgelezen. Er moet echter eerst worden vastgesteld of de gemeten stochast inderdaad normaal verdeeld is. Voor dat doel is er speciaal papier ontworpen met een speciale verticale schaalverdeling (de horizontale verdeling is lineair). Langs de verticale as is de verdeling zo, dat de cumulatieve grafiek van de normale verdeling een rechte lijn wordt. Dit wordt bereikt door de procentlijnen ter weerszijden van de 50%-lijn steeds op groter afstand van elkaar te tekenen. Dergelijk papier wordt normaal-waarschijnlijkheidspapier genoemd. |
| In figuur 11 staat een voorbeeld van normaal-waarschijnlijkheidspapier.Linksboven staat het percentage 0,999 (99,9%); linksonder staat 0,001 (0,1%). De tussenliggende schaalwaarden zijn verder: 1, 10, 20, ..., 90%. Werkwijze
|
figuur 11 |  |
11. Poisson-verdeling
Een veel gebruikte kansverdeling die uit de binomiale verdeling kan worden afgeleid is de
zogenoemde Poisson-verdeling.
We beschrijven de voorwaarden waaronder de Poisson-verdeling kan worden gebruikt.
In een zeker interval I doet een voorval zich gemiddeld l keer voor. Deel je het interval I in n gelijke delen, dan mag je veronderstellen, dat:
- de kans op een voorval voor elk deelinterval even groot is; dus p = l / n
- per deelinterval vindt er hoogstens 1 voorval plaats
- de voorvallen doen zich onafhankelijk van elkaar voor.
Nu is het aantal voorvallen in het gegeven interval een binomiale stochast X met parameters p en n:
| P(X = k) = | (l/n)k (1-l/n) n-k |
We gaan er in hetgeen volgt van uit, dat p = l / n erg klein is (l mag dus niet te groot zijn, terwijl n juist erg groot moet zijn).
Voordat we de kansverdeling van X berekenen, geven we eerst nog (zonder bewijs) een stelling die we bij de berekening zullen gebruiken.
| Stelling 11.1 Voor alle x geldt waarin e het grondtal van de natuurlijke logaritme is.. |
We benaderen nu de kansen voor k = 0, 1, 2, ...
P(X = 0) = (1 - l/n)n. Door
toepassing van stelling 11.1 vinden we nu:
P(X = 0) Ľ e-l
In P(X = 1) = n (l/n)(1 - l/n)n-1 maken we een kleine fout door de
exponent n - 1 te vervangen door n (n is immers erg groot). Dit
geeft dan
P( X = 1) Ľ l e-l
In P(X = 2) = n(n - 1)/2! (l/n)2(1 - l/n)n-2 vervangen we de factor n
- 1 en de exponent n - 2 ook door n zodat
P(X = 2) = l2/2! e-l
Algemeen vinden we dan voor P(X = k)
![]()
Een stochast X met een dergelijke verdeling heet een Poisson-stochast.
Ook voor de Poisson-verdeling zijn cumulatieve tabellen opgesteld, die afhankelijk zijn van de parameter l (zie figuur 12 voor een deel van zo'n tabel).
| figuur 12 |  |
Met dank aan drs. W. Nijdam (afdeling der Toegepaste Wiskunde.
faculteit EWI, Universiteit Twente)
voor zijn waardevolle opmerkingen en aanvullingen.