Lagrange-polynomen
Overzicht ][ Analyse | Cabri | Meetkunde
Deze pagina is geschreven naar aanleiding van de plenaire
lezing van John
Mason (Open University, UK) onder de titel "Probing Polynomials",
op de CabriWorld2004
Conferentie te Rome.
Samenvatting van die lezing:
Polynomials are at the same time the simplest of smooth curves and the context for a range
of perplexing problems which have arisen through the use of Cabri. I intend to raise some
of these problems and to reflect on the notion of mathematics as using natural powers to
make sense of phenomena.
1. CabriJavapplets
Hieronder staan enkele grafieken die geconstrueerd zijn op basis van de theorie
der Lagrange-polynomen (naar Joseph-Louis Lagrange, 1766-1813, Frankrijk).
De grafieken zijn tot stand gekomen volgens een geheel synthetisch-meetkundige
constructie. Voor de beschrijving daarvan wordt verwezen naar de theorie.
Opmerkingen bij de applets
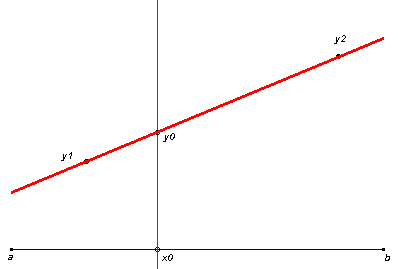
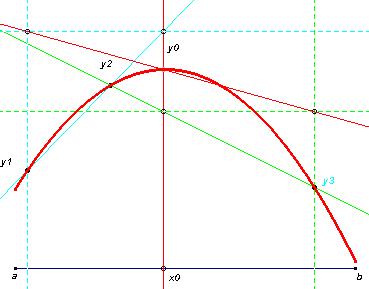
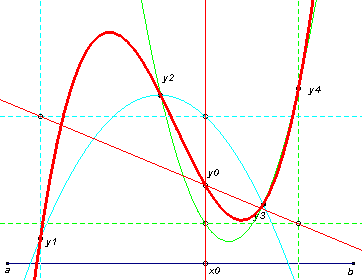
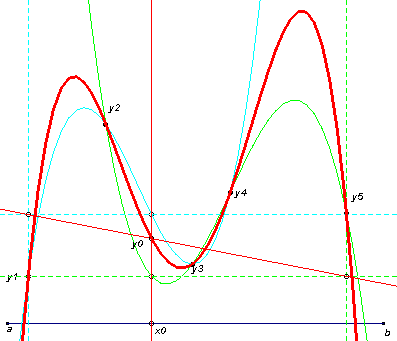
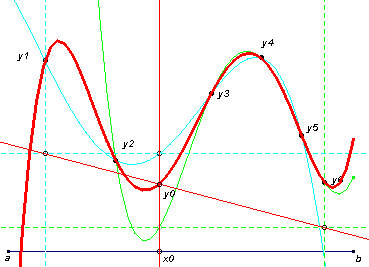
In de applets kunnen de punten y1, y2, y3, ... worden verplaatst. Deze punten zijn de
'basispunten' van het polynoom.
De punten a en b kunnen eveneens worden verplaatst. Deze punten bepalen het interval [a ;
b] waarop de polynoomfunctie is gedefinieerd.
Het punt x0 is het 'aandrijvende' punt van de meetkundige plaats van het punt y0.
2. Theorie
De theorie achter de in paragraaf 1 staande constructies is te vinden in
het artikel "Lagrange-polynomen" (PDF-bestand; ca. 177 kB)
Klik hier om het betreffende
bestand te downloaden (IE-menu: rechtklikken).
3. Download
De figuren waarop bovenbedoelde applets zijn gebaseerd, kunnen in één
bestand via deze website worden gedownload. In dat bestand zijn ook figuren opgenomen die
gemaakt zijn met Cabri Geometry Plus.
Klik hier om het downloaden te starten
(ZIP-bestand; ca. 10 kB).
[p:lagrange.htm] laatste wijziging op: 07-10-2004