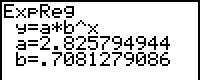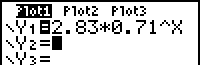TI-83 Werkblad

Overzicht  ][  TI-werkbladen

Overzicht
Bij Moderne Wiskunde A1, deel 1 - Hoofdstuk A4, Exponentiële functies (pag. 114)
Gemengde opdrachten

Opdracht G-1
Hendrik en Sophie hebben beiden al een paar jaar een baan.
Hendriks maandsalaris gaat elk jaar met 54 gulden omhoog.
Sophie krijgt jaarlijks 2% opslag.
In 1997 verdienden zij allebei f 2500,- per maand.
Alle genoemde en te berekenen bedragen zijn nettobedragen.

a. Noem het nieuwe salaris van Hendrik nh en dat van Sophie ns.
Gebruik de variabele t voor jaren.
Geef een formule waarmee je het nieuwe salaris van Hendrik na t jaar kan berekenen:
   nh = 2500 + …
Doe hetzelfde voor het nieuwe salaris van Sophie:
   ns = 2500 . …
b. Voer de formules in op je GR. Gebruik Y1 voor nh en Y2 voor ns.
c. Gebruik de hiernaast staande Window-instelling.
Geef op basis daarvan een schets van de grafieken van nh en ns.
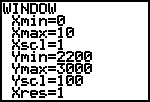Welke conclusie trek je uit de grafieken van de beide functies?		 mw11114-1
d. Bekijk ook de tabel van functiewaarden.
Hoe groot is t in 2000?
Hoe groot is t in 1996?
Geef nu in centen nauwkeurig de maandsalarissen van Hendrik en Sophie in de jaren 2000 en 1996.
e. Bij welke salaris is er sprake van exponentiële groei?
Geef daarbij de groeifactor.
Met welk percentage groeit dat salaris per 10 jaar?

Bij de volgende vraag kan je erg goed gebruik maken van de tabel-functie van de GR.

f.  Zoek uit in welk jaar Sophies maandsalaris hoger wordt dan dat van Hendrik.
Als je gebruik maakt van GR-tabellen, vermeld dan de waarden waaruit je antwoord blijkt.

Ook voor de nieuwe salarissen np en nr van Peter en Rianne hebben we dergelijke formules:
   np = 2450 + 82t
   nr = 2450 . (1,03) t

g. Na hoeveel jaar gaat Rianne meer verdienen dan Peter?
h. Geef een schets van het verloop van de grafieken van np en nr waaruit dit blijkt.

 

Opdracht G-2
Bij het inschenken van een glas bier ontstaat een schuimkraag op het bier.
Na verloop van tijd neemt de hoogte (de dikte) van deze laag af:
tijd in minuten 0 0,5 1,0 1,5 2,0 2,5 3,0
hoogte in cm 2,8 2,4 2,0 1,7 1,4 1,2 1,0
.
a. Waarom is er hier geen sprake van lineaire (negatieve) groei?
Leg uit dat hier mogelijk sprake is van een exponentieel proces.
b. Bereken een groeifactor per halve minuut (in twee decimalen), die van toepassing is bij dit exponentiële proces..
c. Hoe groot is dan de groeifactor per minuut (ook in twee decimalen).
d. Bereken het functievoorschrift voor de hoogte H(t) na t minuten.
Zie eventueel ook hierna: Bij vraag d.
e. Geef met behulp van het functievoorschrift een schatting van de snelheid waarmee de hoogte van de schuimkraag afneemt, als het bier 1 minuut geleden is ingeschonken.
f. Na hoeveel tijd is de hoogte van de schuimkraag minder dan 2 mm?
Opmerking
Als je het antwoord hebt gevonden door gebruik te maken van de tabel-functie van de GR, geef dan de waarden uit de tabel waarop je het antwoord gebaseerd hebt.
Zie eventueel ook hierna: Bij vraag f.

Bij vraag d

Het bovenstaande probleem leent zich goed voor een oplossing van vraag d, waarbij gebruik gemaakt wordt van oa. de LIST-functie van de GR.
Bekijk zo nodig eerst het TI-werkblad over Lijsten.
1. Sla de tijden 0 … 3,0 op in lijst L1.
Maak hierbij zo mogelijk gebruik van de seq-functie. Deze vind je via [LIST]<OPS>5:seq.
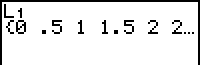Vermeld in dit laatste geval de gebruikte opdracht.		 mw11114-2
2. Sla de hoogtes 2,8 … 1,0 op in lijst L2.
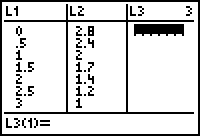Controleer hierna de ingevoerde waarden met [STAT]1:Edit		 mw11114-3
3. Plot de gegevens.
Hierbij is het wellicht nodig de plot-instellingen te wijzigen via [STAT PLOT]1:Plot1.
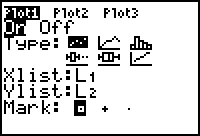Let daarbij vooral op Xlist en Ylist.		 mw11114-4
4. Om de gegevens goed in beeld te krijgen moet je in het [ZOOM] menu de opdracht 9:ZoomStat gebruiken. 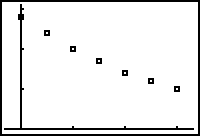mw11114-5
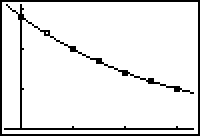mw11114-6

We zullen nu de GR gaan gebruiken om een kromme lijn te tekenen door de geplotte punten, zoals dat in de laatste figuur hierboven is gedaan.
Van deze kromme lijn zullen we eisen dat het de grafiek is van een exponentiële functie.

5. Kies daartoe allereerst [STAT] <CALC>.
In dit menu moet je nu kiezen voor de functie 0:ExpReg.
Dit staat voor "exponentiële regressie".
Regressie is een onderzoek naar het verband tussen twee grootheden. Met de GR wordt dat onderzoek standaard uitgevoerd tussen de waarden in de lijsten L1 en L2.		 mw11114-7
mw11114-8
6. Na het drukken op [0] zien we op het basisscherm (>>>): mw11114-9
7. Na het drukken op [ENTER] zie je (>>>):
De exponentiële regressie is uitgevoerd.
Daarbij is de vergelijking gevonden waarmee de waarden in L2 (y) kunnen worden berekend uit die in L1 (x).
We vinden dus als beginwaarde a = 2,83 (afgerond)
en als groeifactor b = 0,71 (afgerond).
Is de gevonden groeifactor nu de factor per minuut of per halve minuut?		 mw11114-a
8. Je kan nu het gevonden functievoorschrift y = 2,83 . 0,71x invullen in het [Y=] menu: mw11114-b
9. Kies nu weer [GRAPH] en bekijk het gevonden resultaat.

In plaats van stap 8 kunnen we het functievoorschrift ook direct via de GR in het [Y=] menu plaatsen.

8b. Kies [Y=] .
Kies dan [VARS] 5:Statistics…<EQ>.
Kies nu 1:RegEq.
RegEq staat voor Regression Equation (regressievergelijking).		 mw11114-c
Het resultaat in het [Y=] menu is dan (>>>): 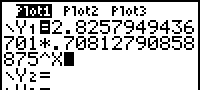mw11114-d

Bij vraag f
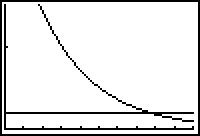
We kunnen vraag f ook beantwoorden door naar het snijpunt van twee grafieken te kijken.
De waarde van x van dit snijpunt kunnen we dan benaderen via [TRACE] .
Welke functievoorschriften moeten we nu in het [Y=] menu vastleggen?		 mw11114-e

We kunnen de x-waarde van het snijpunt ook door de GR laten berekenen.
Dit kan onder andere via het [CALC] menu.
Voorwaarde is dan wel, dat de beide grafieken op de grafische scherm staan (zoals in de figuur hierboven).

Kies nu voor [CALC]5:Intersect en volg de aanwijzingen op het scherm. Sluit daarbij elke vraag af met [ENTER], eventueel na verplaatsing van de schermcursor. mw11114-f

Tenslotte kunnen we de GR ook gebruiken om de vergelijking 2,83 . 0,71x = 0,2 direct op te lossen.
Maar natuurlijk moet je zelf met behulp van logaritmen ook in staat zijn dat te doen.

Hiernaast (>>>) staat de oplossing waarbij gebruik gemaakt is van de "Solver": 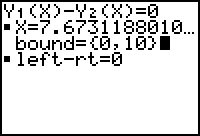mw11114-g

Download
Dit werkblad kan via deze website worden gedownload. Het is alleen beschikbaar in PDF-formaat.
Een PDF-bestand kan met Acrobat® Reader worden gelezen: Get Acrobat® Reader

Download mwa11-114.pdf [ca. 25Kb]

begin pagina

[mw11-114.htm] laatste wijziging op:03-07-00