TI-83 werkblad

Overzicht  ][ TI-werkbladen

Overzicht - Frequentiepolygonen

 terug

Opdracht 1 terug
(Uit: Moderne wiskunde (Wolters-Noordhoff), A1 deel 3, pag. 94, opgave 8)
In de volgende tabel staan de frequenties van leerlingen van een school, ingedeeld naar leeftijd voor het jaar 1990 en een schatting voor het jaar 2000.

leeftijd 1990 2000
12 312 296
13 420 375
14 351 319
15 128 143

¨ Neem de tabel van 1990 over in je rekenmachine (nb. dus alleen 1990).
Je gebruikt hierbij [STAT]1:Edit.
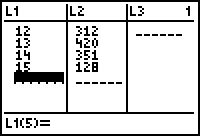Wis indien nodig eerst de in het geheugen staande lijsten met [MEM]ClrAllLists.		 freqpol1
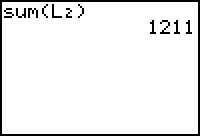
Het totaal van de frequenties kan je berekenen met
[LIST]<MATH>5:sum(		 freqpol2

Afspraak

 terug
De relatieve frequentie van een waarneming (in dit geval is dat een leeftijd) is de frequentie van die waarneming in verhouding tot het totaal.
Relatieve frequenties worden vaak als procenten weergegeven
Voorbeeld
De relatieve frequentie van 12 is gelijk aan 100 x 312/1211 = 25,764.
[einde Voorbeeld]
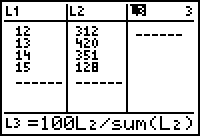
We kunnen de relatieve frequentie eveneens in een lijst zetten.
Daartoe koppelen we een formule aan lijst L3 met
L3 = 100L2/sum(L2).
Plaats de cursor op de naam L3 en typ vervolgens de formule, zoals je hiernaast (>>>) ziet.		 freqpol3
Druk je daarna op [ENTER], dan worden de relatieve frequenties direct berekend. 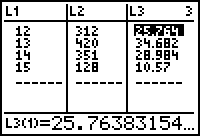freqpol4
Zet de frequenties van het jaar 2000 in lijst L4 en de relatieve frequenties daarvan in lijst L5.
Maak in L6 een tabel waarin voor elke leeftijd in 2000 het percentage staat ten opzichte van dezelfde leeftijd in 1990. 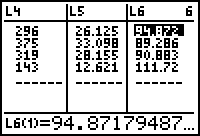freqpol5

terug
We kunnen de gegevens uit (bijvoorbeeld) de lijsten L3 en L5 (de relatieve frequenties dus) ook grafisch weergeven.
We doen dat in een zogenoemd frequentiepolygoon.
We spreken in dit geval van een relatief frequentiepolygoon.
We maken gebruik van het PLOT-menu.
Hiernaast zijn de instellingen voor Plot1 (met de percentages uit L3) en Plot2 (met de percentages uit L5) gegeven.
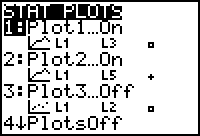In beide gevallen worden ook de gegevens uit L1 gebruikt.		 freqpol6
Opmerking
Het Type van Plot1 en Plot2 is een zogenoemd lijndiagram (Eng: xyLine). Zie het tweede icoon op de eerste rij van de instellingen van de Plots.
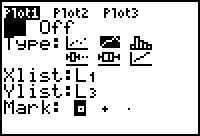[einde Opmerking]		 freqpol7
Het resultaat staat hiernaast (>>>). 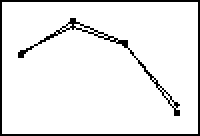freqpol8

Opdracht 2

 terug
(Uit: Moderne wiskunde (Wolters-Noordhoff), A1 deel 3, pag. 95, opgave 10)
In onderstaande tabel staat de opbrengst van tarwe en koren in Nederland in miljoenen kilogrammen.
jaar tarwe koren
1985 851,0 1125,8
1990 1075,9 1347,0
1994 981,0 1263,0
1995 1166,7 1427,2
1996 1268,9 1552,6
.
a. Plot het frequentiepolygoon van de hoeveelheid tarwe over de loop der jaren.
Aanwijzing
Wis eerst de lijsten in het geheugen van de GR.
Plaats de jaren in L1 en de absolute aantallen in L2 en L3.
b. Maak een tabel waarin de relatieve frequentie van de hoeveelheid tarwe ten opzichte van die van koren.
Plot het bijbehorende frequentiepolygoon.
c. Maak een tabel waarin voor elk jaar het percentage van de tarweopbrengst berekend is ten opzichte van de hoeveelheid tarwe in 1985.
Doe dat eveneens ten opzichte van 1995.
d. Plot gelijktijdig de frequentiepolygonen van de percentages uit opgave c en beschrijf de overeenkomsten en verschillen.


Afspraak terug
Onder de somfrequentie of cumulatieve frequentie van een waarnemingsgetal verstaan we de som van alle frequenties vanaf het kleinste waarnemingsgetal tot en met het betreffende waarnemingsgetal.
Voorbeeld
cijfer frequentie somfrequentie relatieve
somfrequentie (%)
4 2 2 7,4
5 3 5 18,5
6 9 14 51,9
7 13 27 100

Als het totaal aantal waarnemingen bekend is (in dit geval 27), dan kunnen we ook de relatieve somfrequentie berekenen.
[einde Voorbeeld]

We kijken nu eerst naar enkele bewerkingen die we met de GR op Lijsten kunnen uitvoeren.

Opdracht 3

 terug
a. Neem de hiernaast staande Lijsten over in je GR.
We willen nu de verschillen berekenen tussen de waarden die in L2 staan.
De TI83 heeft daarvoor een speciale functie, die, zoals zal blijken, voor ons doel echter niet naar wens werkt.
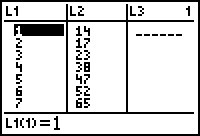
Opmerking: In L1 staan de getallen 1 … 7.		 freqpol9
b. Koppel aan lijst L3 de formule
L3=DList(L2)
De functie D List is te vinden via [LIST]<OPS>7:DList(.		 freqpol10
c. Na [ENTER] zien we het resultaat van de berekeningen (>>>).
In L3 staat op elke positie het verschil tussen de waarde en de waarde op de volgende positie in de lijst.
Merk ook op, dat het aantal elementen van L3 één minder is dan het aantal elementen van L2 (en L1).		 freqpol11

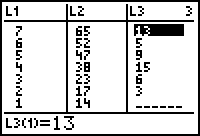
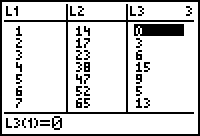
Wat we echter als resultaat willen, is een lijst die er als volgt uitziet:
L1 L2 L3
1 14 0
2 17 3
3 23 6
4 38 15
5 47 9
6 52 5
7 65 13

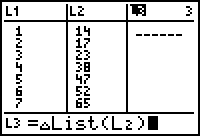
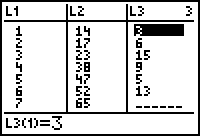
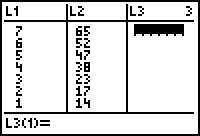
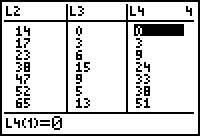
We willen in L3 dus op elke positie (behalve op de eerste, waar een 0 staat) het verschil hebben tussen de waarde in L2 en de waarde op de vorige positie (in L2).

Opdracht 4

 terug
a. Bedenk, voordat je verder leest, hoe je dat met de GR zou kunnen bereiken.
b. Maak Lijst L3 leeg.
Plaats daartoe de cursor op de naam van L3 en druk op [CLEAR], gevolgd door [ENTER].
c. Ga vervolgens naar het rekenscherm en kies daar
[LIST]<OPS>1:SortD(		 freqpol12
d. Vul deze opdracht nu verder aan tot (>>>):
Met de opdracht SortD(L1,L2) wordt de lijst L1 dalend (van groot naar klein) gerangschikt. De waarden in L2 houden daarbij de juiste volgorde.
De D in SortD staat voor het Engelse ‘Descending’.		 freqpol13
e. Resultaat:

Koppel nu aan de naam van L3 de volgende formule:
L3= - DList(L2)
Gebruik het juiste min-teken!

 freqpol14
f. Voeg nu zelf aan het resultaat van deze bewerking de 0 toe op de laatste regel (genummerd met 1).
Dit is noodzakelijk, want anders kan je niet verder!		 freqpol15
g. Sorteer nu de drie lijsten weer opnieuw, maar nu met
SortA(L1,L2,L3)
De A in SortA staat voor het Engelse ‘Ascending’ (oplopend).		 freqpol16
h. We kunnen ook de cumulatieve som van de elementen in een lijst berekenen.
Dit gaat met de functie
[LIST]<OPS>6:cumSom(
Bepaal nu de cumulatieve som van de elementen uit L3 en plaats deze in L4.		 freqpol17a

Opdracht 5

 terug
(Uit: Moderne wiskunde (Wolters-Noordhoff), A1 deel 3, pag. 98, opgave 19)
Veel mensen proberen zuiniger met energie om te gaan. Een goede manier is om te proberen minder gas te verbruiken. Daartoe heeft iemand zijn gasverbruik bijgehouden en op elke eerste dag van de maand de gasmeterstand genoteerd.
regelnummer datum meterstand (m3) verbruik
vorige maand		 totaal verbruik
1 1 aug 2730 - -
2 1 sep 2757 27 27
3 1 okt 2838 81 108
4 1 nov 3027 189 …
5 1 dec 3351 324 …
6 1 jan 3756 405 …
7 1 feb 4188 … …
8 1 mrt 4593 … …
9 1 apr 4944 … …
10 1 mei 5160 … …
11 1 jun 5295 … …
12 1 jul 5376 81 …
13 1 aug 5430 54 2700
.
a. Neem de tabel over en vul hem verder in.
Opmerking
Om eventueel sorteringen (zie Opdracht 4) met de GR uit te voeren is de eerste kolom met regelnummers opgenomen. Plaats deze in L1. Gebruik de lijsten L2, L3, L4 voor opvolgend de meterstand, verbruik vorige maand en totaal verbruik.
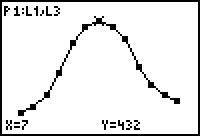
b. Teken een frequentiepolygoon van het gebruik (gebruik lijst L2).
Neem verticaal 1 cm voor 50 m3 en horizontaal 1 cm voor elke maand.
Opmerking
Hieronder (figuur b) staat het polygoon dat wordt verkregen met de GR.
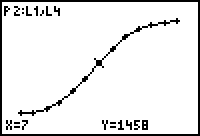
e. Teken een somfrequentiepolygoon voor het totaal verbruik (gegevens staan in L4).
Neem verticaal 1 cm voor 400 m3. Zet de punten boven de rechtergrens van een klasse (maand).
Opmerking
Hieronder (figuur c) staat het somfrequentiepolygoon dat wordt verkregen met de GR.
d. Voeg een kolom toe met daarin het relatieve cumulatieve verbruik.
Zet de gegevens zo nodig in L5.
Opmerking
Hieronder (figuur d) staat het relatieve somfrequentiepolygoon dat wordt verkregen met de GR.
.
figuur b figuur c figuur d
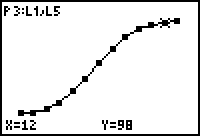freqpol17b freqpol18 freqpol19

Download terug
Deze pagina isNIET MEER beschikbaar in PDF-formaat.

begin pagina
[freqpol.htm] laatste wijziging op: 19-01-18