Stelling van Stewart

Overzicht  ][  Meetkunde

0. Overzicht

  1. Stelling van Stewart
  2. Toepassingen
         2.1. Zwaartelijnformule
         2.2. Bissectriceformule
  3. Naschrift

1. Stelling van Stewart
Voor de berekening van de lengte van hoektransversalen in een driehoek kunnen we gebruik maken van de stelling van Stewart (Matthew Stewart, 1717 - 1785, Schotland).

Stelling
Is X een punt op de zijde AB van driehoek ABC en is AX = p, BX = q en CX = x, dan is
  x2c=a2p + b2q - cpq
Ligt X op het verlengde van AB, dan is
   x2c=a2p - b2q + cpq

Bewijs: zie figuur 1.

figuur 1 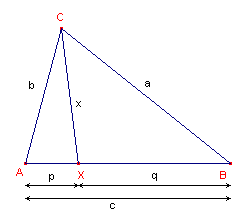stewart1 We passen twee keer de cosinusregel toe:
AXC: x2 = b2 + p2 - 2bp . cos(A)
ABC: a2 = b2 + c2 - 2bc . cos(A)
Eliminatie van cos(A) uit deze vergelijkingen geeft:
   x2c - a2p = b2c - b2p + p2c - c2p
   x2c - a2p = b2(c-p) - cp(c-p)
   x2c - a2p = b2q - cpq
   x2c = a2p + b2q - cpq
figuur 2 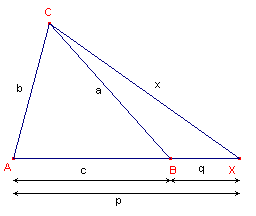stewart2 Toepassing van het hierboven gevondene in driehoek AXC geeft:
   a2p = x2c + b2q - pcq
of
  x2c = a2p - b2q + cpq 
¨

2. Toepassingen
We kunnen stelling 1 toepassen op bijzondere lijnen in een driehoek, zoals op de zwaartelijn en de bissectrice.

2.1. Zwaartelijnformule

figuur 3 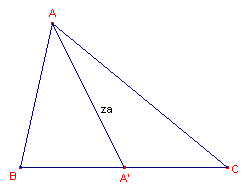stewart3 Volgens stelling 1 is nu:
   za2a = b2 . ½a + c2 . ½a - a . (½a)2
of
   za2 = ½b2 + ½c2 - ¼a2
¨

2.2. Bissectriceformule

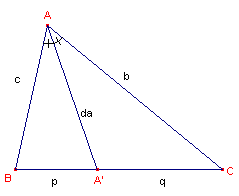figuur 4 stewart4 Volgens stelling 1 hebben we (en we schrijven d voor da):
   d2 · a = b2p + c2q - apq
of
   d2 · a =  b · bp + c · cq - apq ............(x)
Uit de bissectricestelling volgt verder:
   p : q = c : b, zodat bp = cq
In uitdrukking (x) vervangen we nu bp door cq en ook cq door bp.
Uitdrukking (x) is dan gelijkwaardig met:
   d2 · a = b · cq + c · bp - apq
of

   d2 · a = bc(q + p) - apq, en met p + q = a geeft dit:
   d2 · a = bc · a - apq, en dan na deling door a:
   d2 = bc - pq
¨

Opmerking
De bissectriceformule kan ook "elementair" bewezen worden (zie figuur 5).

figuur 5 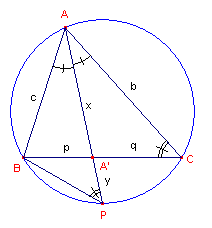stewart5 In driehoek ABC is AA' = x en A'P = y.
Nu is xy = pq ...... volgens de koordenstelling in de omcirkel van ABC ......(1)
Verder is APB ~ ACA', waaruit
   AP : AC = AB : AA' of (x + y) : b = c : x
Met (1) geeft dit:
   (x + pq/x) : b = c : x of  x2 + pq = bc,
zodat
   x2 = bc - pq
¨

[einde Opmerking]

3. Naschrift
Stelling 1 is in 1746 door Stewart, zonder bewijs evenwel, als volgt geformuleerd:

Stelling
Voor drie collineaire punten A,B,C en een willekeurig punt P geldt
 PA2 . BC + PB2 . CA + PC2 . AB + BC . CA . AB = 0
waarbij rekening gehouden is met de richting van de lijnstukken.

In 1751 is de stelling herontdekt en bewezen door Thomas Simpson (1710 - 1761, Engeland), door Leonard Euler (1707-1783, Zwitserland) in 1780 en in 1803 door L.N.M. Carnot (Lazare Nicolas Marguérite Carnot, 1753-1823, Frankrijk).
Het geval waarbij P op de lijn ABC ligt, komt voor in Pappos' Collectio.
De stelling van Stewart wordt ook wel de stelling van Apollonius genoemd.

begin pagina

[stewart.htm] laatste wijziging op: 10-03-05