|
PipeAroundPipe |
||
| Oorspronkelijk (en dat is al weer enkele jaren geleden) heb ik de
figuur op de pagina "DK & Rhinoceros" via
Maple V geprogrammeerd bij gelegenheid van een les
ruimtemeetkunde. De figuur bestaat dus uit een toro´dale spiraal, die zich om een torus wentelt. De Maple V opdrachten zijn eenvoudig: > restart: > with(plots): Definieer een toro´dale spiraal met 20 omwentelingen: > torspiralz20 := [(10+3*sin(20*t))*cos(t), (10+3*sin(20*t))*sin(t),6*cos(20*t)]: Leg de definitie van de ruimtefiguur vast in de variabele rfig1: > rfig1 := spacecurve(torspiralz20,t=0..2*Pi,numpoints=1000,thickness=3, scaling=constrained,axes=frame, color=black): Definieer de torus: > torus:=[10*cos(t),10*sin(t),0]: Leg de definitie van de figuur vast in de variabele rfig2: > rfig2 := tubeplot(torus, t=0..2*Pi, numpoints=1000, radius=2, style=patchnogrid): Teken nu beide figuren in hetzelfde assenstelsel: > display({rfig1, rfig2}, scaling=constrained);
|
|||
Dit resulteert dan in: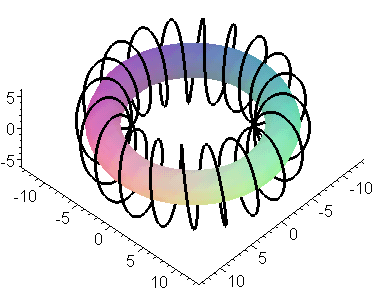 |
|||
In het bovenstaande kunnen we de algemene vergelijkingen van de
beide "ruimtekrommen" gemakkelijk terugvinden: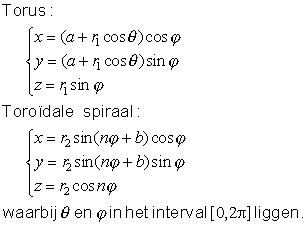 |
[tot.htm] laatste wijziging op: 24-02-02
