|
|
Regelmatige
veelvlakken |
Overzicht |
|
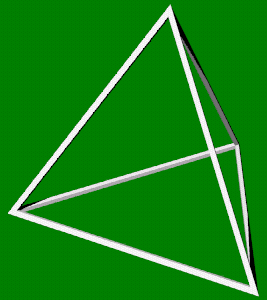 |
Viervlak -
Tetraeder
4 hoekpunten
6 ribben
4 zijvlakken (driehoek)
3 vlakken in een hoekpunt
|
 |
Achtvlak -
Octaeder
6 hoekpunten
12 ribben
8 zijvlakken (driehoek)
4 vlakken in een hoekpunt
|
 |
Twintigvlak -
Icosaeder
12 hoekpunten
30 ribben
20 zijvlakken (driehoek)
5 vlakken in een hoekpunt
|
 |
Kubus -
Hexaeder
8 hoekpunten
12 ribben
6 zijvlakken (vierkant)
3 vlakken in een hoekpunt
|
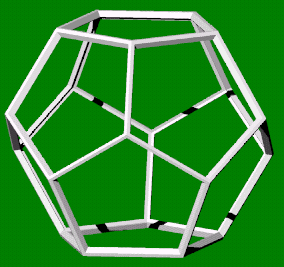 |
Twaalfvlak -
Dodecaeder
20 hoekpunten
30 ribben
12 zijvlakken (vijfhoek)
3 vlakken in een hoekpunt
|
|
Waarom maar
vijf regelmatige veelvlakken? Dit hangt samen met het aantal
zijvlakken dat in hetzelfde hoekpunt samenkomt.
De som van de hoeken daar moet kleiner zijn dan 360º, want anders zouden de
zijvlakken in hetzelfde vlak liggen (of "uitsteken").
Verder moeten in elk hoekpunt minstens 3 vlakken samenkomen. Elke vlakhoek moet dus
kleiner zijn dan 360°/3 = 120°.
Er komen dus slechts drie-, vier- en vijfhoeken als zijvlak in aanmerking.
De hoek van een vijfhoek is gelijk aan 108°. Vier zijvlakken met een vijfhoek kan
niet.
Er is dus slechts 1 regelmatig veelvlak (mogelijk) met een
vijfhoek als "bouwsteen".
De hoek van een vierkant is 90º. Ook hier zijn vier zijvlakken onmogelijk.
Er is dus slechts 1 regelmatig veelvlak (mogelijk) met een
vierkant als "bouwsteen".
Voor de driehoek hebben we:
3 x 60 = 180º; 4 x 60 = 240º; 5 x 60 = 300º.
Er zijn dus 3 regelmatige veelvlakken (mogelijk) met een driehoek
als "bouwsteen".
En dat deze vijf er inderdaad ook zijn, zien we hierboven. |

[regveelvl.htm] laatste wijziging op: 27-12-04





