Moebius-band

Möbius-band

figuur a
moebius1

figuur b
moebius2

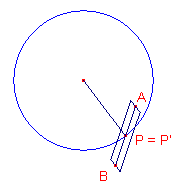
Plakken we van een strook papier de uiteinden (gewoon) aan elkaar dan ontstaat een ring met één binnenkant en een buitenkant.
Wanneer we, voordat we de uiteinden aan elkaar plakken, eerst één van de uiteinden een slag draaien ontstaat een zogenoemde Möbius-band.
Omdat nu de binnen- en de buitenkant in elkaar over gaan, blijft er dus maar één kant over.

Wiskundig gezien kunnen we uitgaan van een rechthoek ABDC (zie figuur a).
Identificeren we A met C en B met D dan krijgen we een ring.
Identificeren we daarentegen A met D en B met C dan krijgen we een Möbius-band (zie figuur b).

figuur c
moebius3

Uit de bovenstaande manier van definiëren volgt, dat de doorsnede van de Möbius-band met een vlak door het middelpunt van de cirkel (bepaald door P en P'; zie figuur a) en een punt van de "definiërende" cirkel, steeds een lijnstuk is met lengte AB.
Geven we de papierstrook een zekere dikte, dan kan de Möbius-band (nu wiskundig gezien een lichaam) worden voortgebracht als de meetkundige plaats van een rechthoekje waarvan het middelpunt P op de cirkel ligt en dat, na één doorloop over de cirkel, 180° gedraaid is (zie figuur c).

figuur d

Op deze manier is de Rhino-afbeelding (gerenderd met Flamingo) in figuur d ontstaan.

Klik hier voor een met Bryce5 gerenderde Rhino-afbeelding.
Klik hier voor een implementatie van de Möbius-band in Maple V (met VRML-plaatje).
Klik hier voor een met Bryce5 gerenderde afbeelding van het oppervlak.

[moebius.htm] laatste wijziging op: 27-12-04