Projectieve kegelsneden
Vooraf | Stellingen ][ Projectieve meetkunde | Meetkunde
1. Vooraf ![]()
Bekendheid wordt voorondersteld met dubbelverhoudingen e.d.
| Definitie Twee lijnenwaaiers zijn projectief als er een 1-1 relatie bestaat tussen de lijnen van die waaiers. |
Een methode om een in de definitie bedoelde 1-1 relatie te verkrijgen is via een
perspectiviteit: tussen twee lijnen, als in onderstaand voorbeeld.
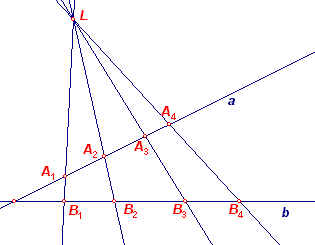
Via de perspectiviteit (L), in de linker figuur, is er een 1-1 relatie tussen de punten A
van de lijn a en de punten B van de lijn b.
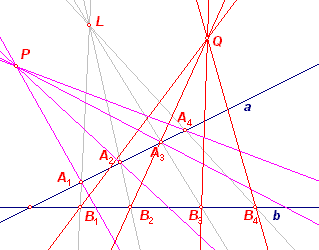
In de rechter figuur is er via de punten reeksen Ai en Bi een 1-1 relatie tussen de lijnen
uit de waaier met top P en de lijnen uit waaier met top Q.
De waaiers (P) en (Q) zijn daarom projectief.
 |
 |
||
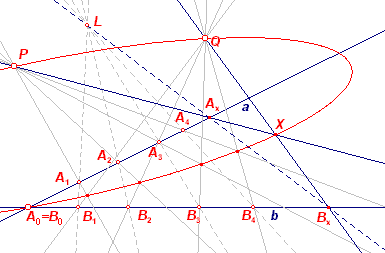 |
In nevenstaande figuur is X = PAx /\ QBx
Bewijs: |
De lijn PQ is een lijn uit waaier (P). Deze lijn snijdt de overeenkomstie lijn uit
waaier (Q) in Q. De kegelsnede gaat dus door Q.
De lijn QP is een lijn uit waaier (Q). Deze snijdt de overeenkomstige lijn uit waaier (P)
in P. De kegelsnede gaat ook door P. ¨
Opmerking
De kegelsnede gaat eveneens door het snijpunt van (de beide punten reeksen op) a
en b.
Immers, daar geldt A0 = B0, zodat PA0 en QA0
elkaar snijden in het snijpunt van a en b.
[einde Opmerking]
| Stelling 2 Een lijn snijdt een kegelsnede in twee punten. |
Bewijs:
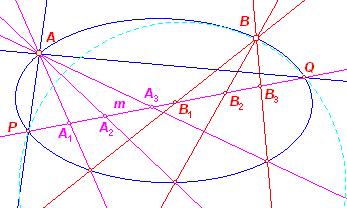 |
Op de snijlijn m liggen twee projectieve puntenreeksen (A, ...
en B, ...). Deze puntenreeksen hebben twee dubbelpunten. Deze dubbelpunten zijn dan de
snijpunten van de lijn m met de kegelsnede. ¨ Opmerking |
| Hulpstelling 3 Zijn E, F en G dubbelpunten van twee puntreeksen op een lijn, dan is elk punt van die lijn dubbelpunt. |
Bewijs:
Stel X en X' zijn twee toegevoegde punten.
Dan is (EFGX) = (E'F'G'X')= (EFGX'), zodat X = X'. ¨
Ontaarde kegelsnede - Als de lijn AB van (A) toegevoegd is
aan de lijn BA van (B), hebben we te maken met een bijzondere kegelsnede.
Zijn nu AP, BP en AQ, BQ twee andere toegevoegde lijnen, en zij R het snijpunt van PQ met
AB.
De waaiers snijden op de lijn PQ een tweetal puntenreeksen in waarbij P, Q, R dubbelpunten
zijn.
Elk punt van PQ is daardoor dubbelpunt (zie Hulpstelling 3). De lijn PQ
ligt dus geheel op de kegelsnede. Ook als we een punt van AB verbinden met A en B, krijgen
we een stel toegevoegde lijnen.
De kegelsnede bestaat dan dus uit de lijnen AB en PQ.
Waarmee bewezen is
| Stelling 4 Als de lijn door de toppen van twee lijnenwaaiers aan elkaar toegevoegd zijn, bestaat de door die waaiers gegenereerde kegelsnede uit twee rechte lijnen. |
| Definitie Een kromme die door een willkeurige lijn gesneden wordt in twee punten, heet kromme van de orde 2. |
| Stelling 5 5.1. Een kegelsnede is een kromme van de orde 2. 5.2. Elke kromme van de orde 2 is een kegelsnede. |
| Stelling 6 Vijf punten bepalen een kegelsnede. |
Bewijs:
Zijn A, B, C, D, E vijf punten, waarvan er geen vier op dezelfde lijn liggen. We
beschouwen nu de waaiers met toppen A en B.
We kiezen nu AC, AD, AE en BC, BD, BE als corresponderen lijnen in de beide waaiers. De
1-1 relatie is hiermee vastgelegd.
Waarmee tevens een kegelsnede door de gegeven vijf punten is bepaald.¨