Pi volgens Archimedes
Overzicht ][ Geschiedenis | Meetkunde
Zie ook de pagina "Oppervlakte van een cirkel"
Zie ook de pagina "Benaderingen van Pi"
1. Inleiding
Van een verloren gegaan boek "De meting van de cirkel" van Archimedes van Syracuse (287-211 vC) is een deel met drie
belangwekkende proposities bewaard gebleven. Deze proposities luiden:
Opmerkingen
[1]
De tekst van propositie II is onvolledig, en daarbij komt dat het bewijs
afhangt van propositie III.
We zullen ons in paragraaf 2 allleen bezighouden met de berekeningen van
Archimedes, die tot het resultaat leiden als vermeld in Propositie III.
[2]
Leonard Euler (1707-1783, Zwitserland) heeft
voorgesteld de verhouding tussen omtrek en middellijn van de cirkel aan te geven met p (in Commentarii Academiae Petropolitanae ad annum 1739,
vol. IX).
[einde Opmerkingen]
Allereerst geven we een Hulpstelling
| Hulpstelling 1: |
Bewijs:
Het bewijs is niet afkomstig van Archimedes. Hij vermeldt het bovenstaande en
gebruikt het zonder meer als uitgangspunt voor de berekeningen die leiden tot Propositie III.
Mogelijk maakte hij gebruik van de volgende formule (die vermoedelijk niet onbekend was in
zijn tijd):
![]()
Nb.
a2 is dus het kleinste
kwadraat onder of boven a2 + b.
[einde Nb.]
Kiezen we a = 2 en b = 1 (en het min-teken), dan volgt uit deze formule
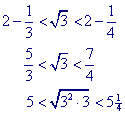
5 is dus een benadering voor Ö27. Met a = 5 en b
= 2 (en het plus-teken) hebben we dan
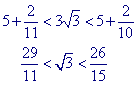
26 is nu een benadering van Ö(152 . 3) = Ö675. Met a = 26 en b = 1 (met een min-teken)
vinden we
![]()
waaruit via deling door 15 volgt
![]() ¨
¨
| 2. Archimedes' benadering voor pi: | |
We volgen hieronder min of meer de tekst van Archimedes, echter voorzien van noodzakelijk commentaar.
Archimedes gaat eerst uit van een om de cirkel beschreven regelmatige
6-hoek. Deze raakt in het punt A aan de cirkel met middelpunt O en straal 1.
De halve zijde van de 6-hoek is AC. Hoek AOC is dus gelijk aan het derde deel van een
rechte hoek (30° zeggen wij).
Daarna deelt hij deze hoek vier keer midden door en krijgt daardoor een regelmatige
96-hoek (zie figuur 1).
| figuur 1 | 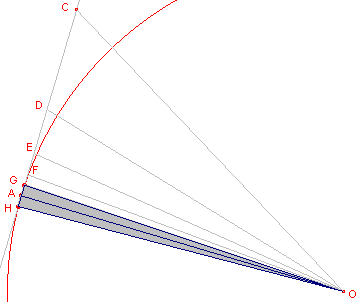 |
Nu is OA : AC = (Ö3 : 1) > 265 : 153 (zie Hulpstelling 1) en OC : CA = 2 : 1 = 306 : 153 Omdat OD bissectrice is van hoek AOC, geldt voor de verhouding van de stukken: CO : AO = CD : AD zodat (CO + AO) : AO = (CD + AD) : AD (CO + AO) : AO = CA : AD (CO + OA) : CA = AO : DA zodat OA : AD > 571 : 153 Archmedes berekent nu verder
|
Daarom, zegt Archimedes, is OD : DA > 5911/8 : 153
(aangezien de wortel uit 349450 groter is dan 5911/8; Archimedes
geeft deze verklaring niet).
Zoals een ondergrens gevonden is voor OD : DA uit OC : CA en de
ondergrens van OA : AC, zo kunnen we dit ook doen voor een ondergrens van OA
: AE en OE : AE uit grenzen van OD : DA rn OA : AD; enzovoorts.
Dit geeft uiteindelijk een ondergrens voor OA : AG.
Ook voor de ingeschreven veelhoek wordt door Archimedes eenzelfde serie benaderigen gegeven (zie figuur 2).
| figuur 2 | 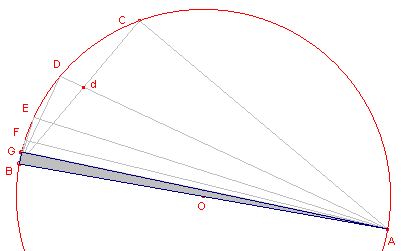 |
ABC is een halve cirkel, waarbij hoek BAC gelijk is aan een derde van een
rechte hoek. Deze hoek wordt ook vier keer middendoor gedeeld. Hierna is BG een zijde van
de ingeschreven 96-hoek. Nu zijn de driehoeken ADB, BDd, ACd gelijkvormig. Dus: AD : DB = BD : Dd = AC : Cd en AC : Cd = AB : Bd (immers Ad is bissectrice) zodat AD : DB = (AB+AC) : (Cd+Bd) = (AB+AC) : BC Maar AC : BC < 1351 : 780 (zie Hulpstelling 1) en BA : BC = 2 : 1 = 1560 : 780. |
Dus: AD : DB < 2911 : 780, zodat
AB2 : DB2 = (29112 + 7802)
: 7802 = 9082321 : 608400
Dus, zegt Archimedes, ook nu zonder toelichting,
AB : BC < 3013¾ : 780
Er ontstaan zo doende dus twee rijen getallen a1, a2, ..., an
en b1, b2, ..., bn, die beide als volgt zijn opgebouwd:
a1 = a0 + b0, a2 = a1
+ b1, ...
waarbij b1 = Ö(a12 + c2),
b2 = Ö(a22+c2), ...
met a0 = 265, b0 = 306, c = 153 voor de omgeschreven cirkel
en a0 =1351, b0 = 1560, c = 780 voor de ingeschreven
cirkel.
De waarden die Archimedes vindt, zijn opgenomen in de volgende tabel
| n | omgeschreven veelhoek |
an | bn | c | ingeschreven veelhoek |
an | bn | c | ||
| 0 | 6 | 265 | 306 | 153 | 6 | 1351 | 1560 | 780 | ||
| 1 | 12 | 571 | Ö(5712+1532) > 5911/8 |
153 | 12 | 2911 | Ö(29112+7802) < 30133/4 |
780 | ||
| 2 | 24 | 11621/8 | Ö(11621/82+1532) > 23391/4 |
153 | 24 | 59123/4 1823 |
(zie Opmerking 1) Ö(18232 + 2402) < 18389/11 |
780 240 |
||
| 3 | 48 | 23341/4 | Ö(23341/42+1532) > 23391/4 |
153 | 48 | 36619/11 1007 |
(zie Opmerking 1) Ö(10072 + 662) < 10091/6 |
240 66 |
||
| 4 | 96 | 46731/2 | 153 | 96 | 20161/6 | Ö(20161/62+662) < 20171/4 |
66 | |||
Opmerkingen
[1]
Archimedes vereenvoudigt de verhouding a2 : c met de
factor 4/13 en de verhouding a3 : c met de
factor 11/40 alvorens verder te rekenen.
[2]
Bij geen van de afschattingen van de wortels in bovenstaande tabel geeft Archimedes uitleg
over de gevonden waarde.
We kunnen echter aannemen, dat hij gebruik maakte van de formule (a ± b)2
= a2 ± 2ab + b2.
[einde Opmerkingen]
Bij de omgeschreven veelhoek is de laatste verhouding a4 : c gelijk
aan de verhouding OA : AG = 2OA : GH (GH in figuur 1
is de zijde van de 96-hoek); bij de ingeschreven veelhoek is de verhouding b4
: c gelijk aan AB : BG (BG in figuur 2 is de zijde van de
96-hoek).
Zodat we uiteindelijk vinden
![]()
| Archimedes leidt hieruit zonder meer uit af, dat | |
Opmerking
Mogelijk heeft Archimedes de waarde 31/7 afgeleid uit het feit, dat ![]() .
.
De waarde 310/71 is wellicht gevonden als deel van de kettingbreuk
voor 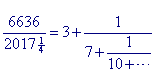 .
.
[einde Opmerking]
3. Een iets andere benadering
Uit de lengte van de zijde van een regelmatige n-hoek (die om- of ingeschreven is) kunnen
we eenvoudig de lengte van de zijde van de 2n-hoek afleiden (zie figuur 3).
| figuur 3 | 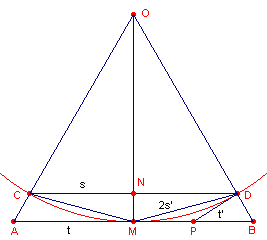 |
AB = 2t is de zijde van de omgeschreven n-hoek. CD = 2s is de zijde van de ingeschreven n-hoek. Nu is DP = t' de halve zijde van de omgeschreven 2n-hoek (P op BM). DM = 2s' is de zijde van de ingeschreven 2n-hoek. Uit de gelijkvormigheid van de driehoeken BDP en BMO volgt nu PD : PB = OM : OB of t' : (t - t') = OM : OB Verder is ND : MB = OD : OB = OM : OB = s : t |
Zodat
s / t = t' / (t - t')
waaruit volgt t' = ts / (t + s) .....(1)
Uit de gelijkvomigheid van de driehoeken CMD en DPM volgt
CM : CD = DP : DM
of
2s' : 2s = t' : 2s'
waaruit st' = 2 (s')2 ..... (2)
Stellen we nu a gelijk aan de omtrek van de ingeschreven veelhoek en b
gelijk aan die van de omgeschreven veelhoek en a' en b' die van de
bijbehorende 2n-hoek, dan is dus
a = n . 2s en a' = 2n . 2s'
b = n . 2t en b' = 2n . 2t'
Hieruit kunnen we dus recursieve betrekkingen vinden tussen a', b', a en b (door
eliminatie van n, s, s', t, t' uit bovenstaande betrekkingen):
Nu is s' = a'/4n en t' = b' / 4n
Substitutie in (1) geeft b' / 4n = (ab /4n2)
/ (b/2n + a/2n) oftewel
b' = 2ab / (a + b)
Substitutie in (2) geeft
a/2n . b'/4n = 2a' 2/4n2
oftewel a' 2 = ab', zodat
a' = Ö(ab')
We zijn hiermee in staat opvolgende benaderingen voor p
te berekenen (beginwaarden: a = 3, b = 2Ö3)
6-hoek: a = 3.000000000, b
= 3.464101615
12-hoek: a = 3.105828542, b =
3.215390310
24-hoek: a = 3.132628614, b =
3.159659942
48-hoek: a = 3.139350204, b =
3.146086216
96-hoek: a = 3.141031952, b =
3.142714600
Klik hier voor de berekening van deze waarden met behulp van Maple V.
Opmerking
Bovenstaande berekeningsmethode staat ook bekend onder de naam Borchardt-Pfaff
algorithme.
[einde Opmerking]
| Hulpstelling 2 2xy / ( x + y ) < Ö(xy) of het harmonisch gemiddelde van twee getallen is kleiner dan het meetkundig gemiddelde. |
Bewijs:
Uit (Öx - Öy)2
> 0 volgt 2Ö(xy) < x + y. Vermenigvuldiging met
Ö(xy)/(x + y) geeft de betrekking als
vermeld in de stelling. ¨
Voor de in paragraaf 3 gevonden betrekkingen
(1) b' = 2ab / (a + b)
(2) a' = Ö(ab')
vinden we nu op basis van Hulpstelling 2:
(1a) b' < wrt(ab), zodat b' 2
< ab
Uit (2) geschreven als a' 2 = ab', vinden we
met (1a), na vermenigvuldiging van beide leden: a' 2b' 2
< a2bb' of a' 2b'
< a2b.
Schrijven we 3Ö(a2b)
= B en 3Ö(a' 2b')
= B', dan staat er dus B' < B.
Op basis van Hulpstelling 2 en (2) vinden we
(2a) a' > 2ab' / (a + b'), zodat 2 / a' < (a +
b')/ab' = 1/a + 1/b'.
We hebben echter ook de betrekking 2/b' = (a + b)/ab = 1/a + 1/b
(deze volgt uit (1)).
Tellen we deze relatie bij die in (2a) op, dan staat er:
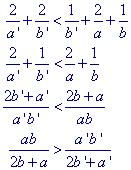
Schrijven we A = 3ab / (2b+a) en B' =
3a'b' / (2b' + a'), dan blijkt hieruit, dat A'
> A.
Zij nu O de omtrek van de cirkel, dan geldt A < O < B.
Gebruiken we de waarden A, A' en B, B' nu recursief dan vinden we voor de benadering van p, weer uitgaande van dezelfde startwaarden a = 3,
b = 2Ö3 als in paragraaf 3:
6-hoek: A = 3.000000000, B
= 3.464101615
12-hoek: A = 3.140237344, B =
3.147345190
24-hoek: A = 3.141509994, B =
3.141927919
Klik hier voor de berekening van deze waarden met behulp van Maple V.
We zien dus dat nu bij de benadering via de regelmatige 12-hoek reeds 2 significante decimalen gevonden worden (dit was bij de methode in paragraaf 3 pas bij de regelmatige 96-hoek het geval)..
[piarchi.htm] laatste wijziging op: 15-07-2000