Ontbinden in factoren
Distributieve eigenschap | Ontbinden ][ DK en Algebra
1. Distributieve eigenschap van de
vermenigvuldiging ![]()
Voor de rekenkundige bewerkingen x en + binnen de verzameling
van de reŽle getallen geldt de distributieve eigenschap
a x (b + c) = ab + ac
en vanwege de commutativiteit van de vermenigvuldiging geldt ook
(b + c) x a = ba + ca
= ab + ac
We kunnen dit fraai illustreren met de volgende figuur, waarin we oppervlaktes van
rechthoeken met elkaar vergelijken.
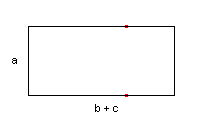
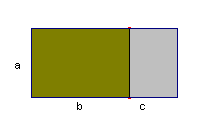
| figuur 1 | rechthoek met zijden a en b+c |
een rechthoek met zijden a en b en een rechthoek met zijden a en c |
 |
 |
Lezen we de distributieve eigenschap van rechts naar links, dan spreken we ook wel van ontbinden
in factoren.
De optelling ab + ac is geschreven als een vermenigvuldiging met behulp
van de factoren a en b+c.
Passen we de distributieve eigenschap twee keer toe op de uitdrukking
(a + p) x
(b + q)
dan krijgen we
(a + p) x
(b + q) = (a+p)b + (a+p)q = ab + pb + aq + pq
Ook nu kunnen we dit eenvoudig inzien met oppervlaktes:
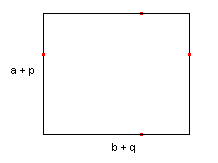
| figuur 2 | rechthoek met zijden a+p en b+q |
rechthoeken met zijden a,b en p,b en a,q en p,q |
 |
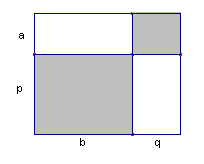 |
2.1. Standaard ontbinding, merkwaardige producten
![]()
| Definitie Ontbinden in factoren is het schrijven van een uitdrukking als een product (vermenigvuldiging) met factoren ongelijk 1. |
In paragraaf 1 hebben we de volgende ontbindingen reeds leren kennen:
| I | ab + ac = a(b + c) ab + ac + ad = a(b + c + d) - deze ontbindingen heten standaard ontbindingen |
| II | ab + pb + aq + pq = a(b+q) +p(b+q) = (a + p)(b + q) |
Opmerking
Bij de standaard ontbindingen spreekt men van een "echte" ontbinding, indien de
termen van de haakjesvorm geen gemeenschappelijke factoren hebben.
Voorts geldt min of meer bij afspraak, dat er in de haakjesvorm geen breuken voorkomen.
[einde Opmerking]
Voorbeelden
10a2b2 - 1/5ab2c = 1/5ab2
(50a - c)
3/5a3x3 - 1/10a2x2
+3/4ax =1/20ax(12a2x2 -
2ax + 15)
90x3 + 40x2y2 - 126xy - 56y3 = 10x2(9x + 4y2)
- 14y2(9x + 4y2) = 2(5x2 - 7y2)(9x + 4y2)
[einde Voorbeelden]
We leiden hieronder nog enkele belangrijke producten, de merkwaardige producten, en de daarbij behorende ontbindingen af.
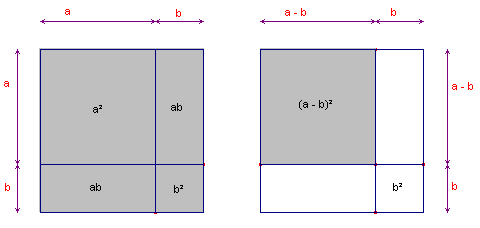
| (a + b)2 = (a+b)(a+b) = (a+b)a + (a+b)b = a2 + ab + ab + b2 = a2 + 2ab + b2 (zie figuur 3, links) |
| (a - b)2 = (a-b)(a-b) = (a-b)a - (a-b)b = a2 - ab - ab + b2 = a2 - 2ab + b2 (zie figuur 3, rechts) |
| (a - b)(a + b) = (a-b)a + (a-b)b = a2 - ab + ab - b2 = a2 - b2 (zie figuur 4) |
figuur 4 |
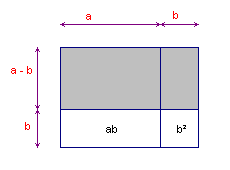 |
De oppervlakte van de grijze rechthoek hiernaast is: (a - b)(a + b) Maar deze is ook gelijk aan a(a + b) - ab - b2 = a2 - b2 |
Lezen we bovenstaande betrekkingen weer van rechts naar links dan vinden we
| IIIa | a2 + 2ab + b2 = (a + b)2 |
| IIIb | a2 - 2ab + b2 = (a - b)2 |
| IV | a2 - b2 = (a - b)(a + b) |
De betrekkingen I t/m IV worden gebruikt om mogelijke ontbindingen in factoren (snel) te herkennen.
2.2. Ontbinden van een kwadratische vorm ![]()
| V | a2 + (p+q)a + pq = (a + p)(a+q) |
| figuur 5 | 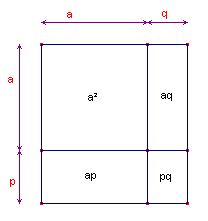 |
Uit figuur 5 zien we dat deze ontbinding juist is. In voorkomende gevallen behoeft men slechts de laatste term pq (bij rangschikking naar afdalende machten) in twee factoren te ontbinden, die samen de cofactor zijn van de eerste macht. Voorbeelden |
Deze vorm kan, indien het aantal ontbindingen van pq (in twee factoren) groot
is, ook op een andere manier worden behandeld.
We bekijken dan in eerste instantie alleen de eerste twee termen (de termen met een x) en
vullen deze aan tot een volledig kwadraat.
[3]
x2 + 12x - 864 = (x2 + 12x + 36)
- 36 - 864 = (x + 6)2 - 900 =
(x + 6 - 30)(x + 6 +30) =
(x - 24)(x + 36)
[einde Voorbeelden]
(wordt voortgezet)
[ontbinden.htm] laatste wijziging op: 11-02-2001