Fouten
Inleiding | Absoluut en relatief | Significantie | Sommatie ][ Numerieke wiskunde
1. Inleiding ![]()
Bij het rekenen moet men de nauwkeurigheid, die men bereiken wil of bereiken kan steeds in
het oog houden. Men moet dan ook rekening houden met de oorzaken van het optreden van
onnauwkeurigheden.
Deze kunnen tot de volgende fouten aanleiding geven:
a. grove fouten
b. inherente fouten
c. afrondingsfouten
d. procesfouten
a. Grove fouten of abuizen
Deze kunnen ontstaan door tekortkomingen van de rekenaar (of programmeur), waardoor bij
het opstellen van het rekenprogramma fouten insluipen. Zij kunnen worden ingeperkt door
hetzelfde probleem door verschillende rekenaars (programmeurs) onafhankelijk van elkaar te
laten uitwerken, of door een complementair rekenprogramma op te stellen, waarbij de
gevonden uitkomsten op hun juistheid worden onderzocht.
Bij het oplossen van een hogere machtsvergelijking kan men bijvoorbeeld de uitkomsten
verifiėren door deze in de vergelijking te substitueren.
Als het resultaat van een berekening een serie uitkomsten geeft, dan zal deze rij van
getallen in het algemeen vloeiend verlopen. Springen er waarden uit, dan is dit meestal
een aanwijzing, dat er iets mis gegaan is bij de berekening. Systematische fouten,
bijvoorbeeld door een verkeerde opzet van de formules, worden op deze manier echter niet
ontdekt.
b. Inherente fouten
Dit zijn fouten in de gegevens, waarvan men uitgaat. Zijn dit bijvoorbeeld meetwaarden,
dan zit in deze metingen op zichzelf al een zekere onnauwkeurigheid.
De uitkomsten van het rekenproces hebben hoogstens dezelfde graad van nauwkeurigheid als
de begingegevens. Inherente fouten kunnen aIleen worden verkleind door de gegevens
nauwkeuriger te maken.
c. Afrondingsfouten
Deze hebben betrekking op de getallen. Door de beperktheid van de hulpmiddelen moeten de
getallen op een zeker ogenblik worden afgerond. De fout, die hierdoor ontstaat, is
hoogstens gelijk aan een halve eenheid van de laatste decimaal.
Afrondingsfouten kunnen dus verkleind worden door meer decimalen in de berekening mee te
nemen.
d. Procesfouten (Engels: truncation errors)
Deze fouten hebben betrekking op de gebruikte formules. Het zijn fouten die ontstaan,
doordat verschillende analytische formules door benaderingsformules
worden vervangen: eindige reeksen in plaats van oneindige reeksen, eindige sommen in
plaats van integralen, enz.
Bovenstaande fouten hebben vaak een grote invloed op de uitkomsten.
| Definitieformule Werkelijke waarde = Benaderde waarde + Fout |
Voorbeeld
We definieren e-x met x > 0 als de som van de
oneindige alternerende reeks
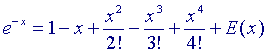
In verband met het alterneren van de reeks kan de fout als volgt worden afgeschat:
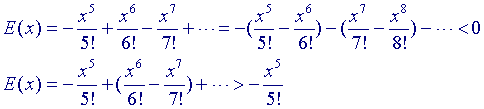
Breken we de oneindige reeks bij de 5e term af, dan is dus
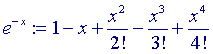
(:= betekent hier: "is bij benadering gelijk aan").
De negatieve fout is dan absoluut kleiner dan x5/120.
Voor (bijvoorbeeld) x = 1/3 vinden we:
![]()
De procesfout ligt hier tussen 0 en -1/29160 := 0,000034.
De grootste waarde van de procesfout is dus gelijk aan 3,5 · 10-5.
De afrondingsfout onstaat doordat bij de berekening de getallen 1/3,
1/18, ... uit de reeks worden geschreven als decimalen.
Ronden we af op (bijvoorbeeld) 5 decimalen, dan is de fout van elk van de breuken gelijk
aan 0,5 · 10-5.
De fout in het antwoord, hierdoor veroorzaakt, is dus hoogstens gelijk aan 4 · 0,5 · 10-5
= 2 · 10-5.
In dit geval geven de procesfout en de afrondingsfout samen een maximale fout van
3,5 · 10-5 + 2 · 10-5
= 5,5 · 10-5
Dit houdt in, dat in de som van de 5 termen, 0,71657, de 5e decimaal onbetrouwbaar is.
De 4e decimaal kan dus een 5 of een 6 zijn.
We kunnen tegen een inherente fout aanlopen, als we de exponent 1/3
bij de berekening afronden tot (bijvoorbeeld) 0,3333.
De werkelijke waarde van de exponent ligt tussen 0,3333 en 0,3334.
De fout in de exponent, I(x), is dan maximaal 0,5 · 10-4
(of beter: 0,34 · 10-4).
De inherente fout I(e-x) in de functie e-x
kunnen we nu als volgt bepalen (benaderen):
I(e-x) = e-(x + I(x))
- e-x = e-x · (e-I(x)
- 1) := - e-x · I(x)
Gaan we uit van e-x = 0,7166, dan is
I(e-x) := - e-x · I(x)
:= 0,72 · 0,5 · 10-4 =
0,36 · 10-4.
| Definitie De ware fout van een benadering van een getal is het absolute verschil tussen de werkelijke waarde a en de benaderde waarde a'. |
Omdat de ware fout in het algemeen niet berekend kan, worden wordt meestal een afschatting van de fout gemaakt. Men geeft dan orde van grootte van de maximale fout aan.
| Definitie Is a een getal en a' een benadering van dat getal met |a - a'| £ E(a'), dan heet E(a') een (de) absolute fout van de benaderde waarde a'. |
Opmerkingen
[1]
De absolute fout van een benadering is niet ondubbelzinnig bepaald.
Zo is bijvoorbeeld 2/7 := 0,2857 (in 4 decimalen nauwkeurig).
Als absolute fout kunnen bijvoorbeeld de waarden 0,2 · 10-4
en ook 0,5 · 10-4 worden genomen.
Meestal tracht men een zo klein mogelijke bovengrens voor de absolute fout te geven. In
dit geval spreek men toch vaak van de absolute fout.
[2] Schrijfwijze
Is E(a') de absolute fout van de benadering a' van een getal a,
dan schrijft men a = a' ± E(a').
[einde Opmerkingen]
| Definitie Is a' een benadering van het getal a, met een absolute fout E(a'), dan heet het getal R(a') = E(a') / |a'| een relatieve fout van a'. |
Voorbeeld
3,14 en 3,14159 zijn benaderingen van het getal p.
In dit geval kunnen we de ware fout zeker niet aangeven. We kunnen we schrijven:
p = 3,14 ± 0,16 · 10-2.
Een absolute fout in 3,14 is dus (bijvoorbeeld) 0,16 · 10-2.
In dit geval is de relatieve fout gelijk aan 0,16 · 10-2 / 3,14
:= 0,51 · 10-3 (= 0,051%).
| Definitie Een getal a heeft n betrouwbare of significante cijfers, als het n-de cijfer in de (decimale) schrijfwijze van a hoogstens een halve eenheid fout is. Daarbij tellen alle nullen die links van het eerste van nul verschillend cijfer staan, niet mee. |
Voorbeelden
[1]
a = 0,72626 ± 0,3 · 10-5
In deze schrijfwijze zijn 5 cijfers significant (van links af: 7, 2, 6, 2, 6).
[2]
a = 0,0079626 ± 3,6 · 10-6
In deze schrijfwijze zijn 3 cijfers significant (van links af: 7, 9, 6).
[einde Voorbeelden]
Door afronden kunnen we ervoor zorgen, dat een benadering b' van een getal b uitsluitend geschreven wordt met significante cijfers.
Voorbeeld
b = 0,07963 ± 0,8 · 10-5
b = 0,0796 ± 0,3 · 10-4
b = 0,080 ± 0,4 · 10-3
Het getal b' = 0,080 is in drie decimalen nauwkeurig. b' heeft 2
significante cijfers (van links af: 8, 0).
4. Sommatie van benaderingen ![]()
Is a' een benadering van a met een absolute fout E(a') en b'
een benadering van b met een absolute fout E(b'), dan is
|a - a'| £ E(a')
en |b - b'| £ E(b').
Hieruit volgt:
| (a ± b) - (a' ± b') | = | (a - a')
± (b - b') | £ |a - a'|
+ |b - b'| £ E(a') + E(b')
Dus:
De absolute fout van de som (of het verschil) van twee benaderingen is gelijk aan de
som van de absolute fouten van die benaderingen.
Bepalen we nu de som van n benaderingen, waarvan de absolute fout van elk
getal gelijk is aan f (>0), dan is de maximaal mogelijke fout gelijk aan pm nf.
Is bijvoorbeeld n =1000 en f = 0,5 · 10-3,
dan is de maxiaal mogelijke fout in de som ± 0,5.
Nu is het niet erg waarschijnlijk, dat de fout inderdaad zo groot zal zijn.
Als we aannemen, dat de fouten willekeurig verdeeld zijn over het interval [-f
; f], dan vinden we met behulp van kansrekening, dat de (meest) waarschijnlijke
fout (de standaardafwijking van de fouten) gelijk is aan
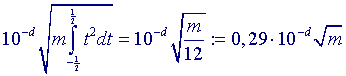
bij afronding op d decimalen.
[fouten.htm] laatste wijziging op: 23-09-00