Cirkelsector en cirkelsegment

Overzicht  ][  Meetkunde | Analyse

---

Overzicht

1. Inleiding
2. Betrekkingen en berekeningen
3. Oppervlakte met integraalrekening
4. Referenties

---

1. Inleiding

Definitie Een cirkelsector is een deel van het cirkeloppervlak ingesloten door een cirkelboog en de beide stralen naar de eindpunten van die cirkelboog. Een cirkelsegment is een deel van het cirkeloppervlak ingesloten door een cirkelboog en de koorde tussen de eindpunten van die cirkelboog. Nb. Beide vlakdelen zijn met bovenstaande definitie niet eenduidig bepaald.

De middelpuntshoek op de cirkelboog wordt meestal aangegeven met de Griekse letter q (thèta). Daarbij geldt dan : 0 < q £ p.
Is q = p dan spreken we meestal van een halve cirkel.

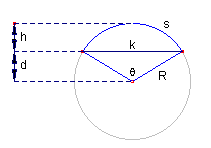Verdere naamgeving: k - lengte van de koorde s - lengte van de cirkelboog h - hoogte van het segment (ook van het segmentdeel van de sector) d - afstand van het middelpunt van de cirkel tot de koorde R - straal van de cirkel

2. Betrekkingen en berekeningen
We hebben nu de volgende betrekkingen tussen de verschillende elementen:

R	=	h + d
s	=	Rq		immers, s / (2pR) = q / (2p)
d	=	R cos(½q)		volgt uit hoekeigenschappen (goniometrie)
	=	½k cot(½q)		volgt uit hoekeigenschappen (goniometrie)
	=	Ö(R2 - 1/4 k2)		volgens de stelling van Pythagoras
k	=	2R sin(½q)		volgt uit hoekeigenschappen (goniometrie)
	=	2d tan(½q)		volgt uit hoekeigenschappen (goniometrie)
	=	2Ö(R2 - d2)		volgens de stelling van Pythagoras
	=	2Ö(2Rh - h2)		voor d = R - h is R2 - d2 = R2 - (R2 - 2Rh + h2) = 2Rh - h2
q	=	s / R		volgt uit s = Rq
	=	2arcsin(k/(2R))		volgt uit k = 2R sin(½q)
	=	2arccos(d/R)		volgt uit d = R cos(½q)
	=	2arctan(k/(2d))		volgt uit k = 2d tan(½q)

Voor de oppervlakte V(sector) en V(segment) hebben we de volgende formules:

V(sector)	=	½Rs		immers V(sector) = s / (2pR) . pR2 (verhouding tussen omtrek en oppervlakte)
	=	½R2q		volgt uit s = Rq
V(segment)	=	V(sector)-V(driehoek)		nu geldt: V(driehoek) = ½R2sin(q)
	=	½R2(q - sinq)		immers uit de vorige regel volgt:  V(segment) = ½R2q - ½R2sin(q)
	=	½(Rs - kd)		immers s = Rq en V(driehoek) = ½kd
	=	R2arccos(d/R) - dÖ(R2 - d2)		immers V(sector) = ½R2q met q = 2arccos(d/R)
	=	R2arccos((R - h)/R) - (R - h)Ö(2Rh - h2)		immers d = R - h
	=	R2arcsin( k/(2R) ) - ½kd		volgt uit V(segment) = ½Rs - ½kd en s = Rq  = 2Rarcsin( k/(2R) )

3. Oppervlakte met integraalrekening
We kunnen de oppervlaktes ook met behulp van de integraalrekening afleiden.

Oppervlakte sector

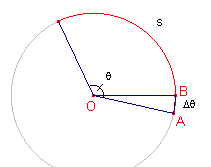Voor driehoek OAB met rechte hoek A (zie figuur hiernaast) geldt: AB » Dq, zodat V(OAB) = ½R . Dq. Waaruit volgt: 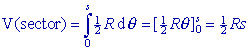Deze formule hebben we hierboven eenvoudiger gevonden.

Oppervlakte segment

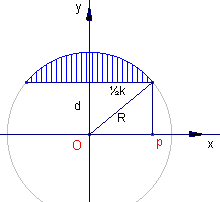Zij p = ½k. Dan geldt voor V(Segment): 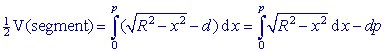We berekenen de eerste term van het rechter lid (de integraal) dmv. subsitutie van x = Rcos(u) met dx = -Rsin(u) . du. We krijgen dan: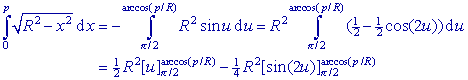

Uitwerking van dit laatste geeft voor de waarde van de integraal, aangegeven met I:

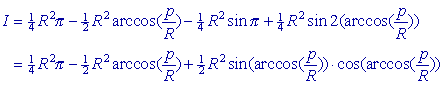
Wegens cos(arccos(p/R))= p / R en sin(arccos(p/R)) = sin(½p - ½q) = cos(½q) = d / R vinden we dan:

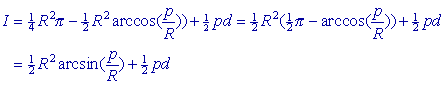
Zodat

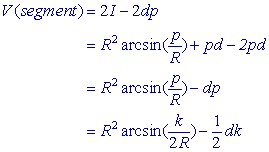
Deze formule hebben we hierboven heelwat eenvoudiger gevonden.

3. Referenties

[1]		M.R. SPIEGEL, J. LIU: Mathematical Handbook of Formulas and Tables, Schaum's Outline Series (McGraw Hill, New York)
[2]		ERIC WEISSTEIN: World of Mathematics - Math World (Wolfram Research) / Segment / Sector
[2]		J.C.A. WEVERS: Wiskundig Formularium (PDF-bestand, Nederlands en Engels)

---

[cirkelsect.htm] laatste wijziging op: 11-11-02