Benaderingen van de wortels van een vergelijking

Overzicht ][ Numerieke wiskunde

 [ deze pagina is nog in bewerking ] 

Overzicht begin pagina

  1. Inleiding
  2. Lokaliseren van wortels
       2.1. Grafische methode
       2.2. Weglaten of schatten van termen
  3. Lineaire interpolatie
  4. Newton-Raphson

1. Inleiding begin pagina
Het (methodisch) oplossen van vergelijkingen in de schoolwiskunde beperkt zich in het algemeen tot zogenoemde algebraïsche vergelijkingen (vergelijkingen waarin alleen algebraïsche bewerkingen, zoals de optelling en vermenigvuldiging, voorkomen).
In een enkel geval komen ook transcendente vergelijkingen aan de orde (zoals 1/2log(x) - 2x = 0).
Deze laatste worden dan meestal opgelost door middel van de methode van inklemmen.
Methodieken voor benaderingen anders dan deze worden meestal niet behandeld.
In het onderstaande trachten we daaraan iets (niet uitputtend dus) te doen.

2. Lokaliseren van wortels begin pagina
2.1. Grafische methode
We gaan daarbij uit van de vergelijking f(x) = 0
We onderscheiden dan twee, niet echt verschillende, methoden:

2.1.1. Tekenen van de grafiek van y=f(x) en bepaling (benadering) van de snijpunten van de grafiek met de x-as;
2.1.2. Splitsen van de de vergelijking in f1(x) = f2(x), het tekenen van de grafieken van beide functies, gevolgd door het benaderen van de x-waarden van de snijpunten van die twee grafieken.

In beide gevallen kan de benadering, bij een nauwkeurige weergave van de functies, uit de grafiek worden afgelezen (eventueel via meting).

Voorbeeld
We hebben sin(x) - (x + 1)/(x - 1) = 0
We passen de methode genoemd bij 2.1.2 toe.
We splitsen nu als sin(x) = (x + 1)/(x - 1)
De wortels van de vergelijking zijn dan de x-waarden van de snijpunten van de grafieken van y = sin(x) en y = (x + 1)/(x - 1); zie daartoe figuur 1.

figuur 1 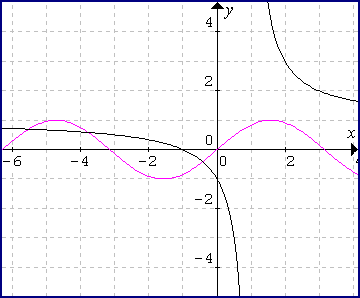benader1 We zien nu uit de grafiek, dat er wortels liggen in de intervallen (-pi/2, 0), (-3pi/2, -pi), (-2pi, -3pi/2), ...

Schattingen (na meten in de grafiek) zijn:
x = 0,3 ; x = -3,8 ; x = -5,5 ; enz.

2.2. Weglaten of schatten van termen begin pagina
We kunnen in een aantal gevallen een deel (of delen) van de vergelijking vervangen door constanten.
We lichten dit toe aan een voorbeeld.

Voorbeeld
We hebben x2 - 10log(x) = 10.
Bekijken we de functie f(x) = x2 - 10log(x) - 10.
Voor 1 < x < 10 hebben we 0 < 10log(x) < 1.

figuur 2 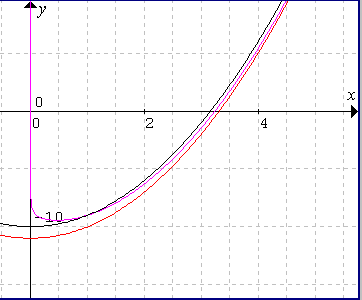benader2 Waardoor voor x in <1 ; 10> geldt:
   x2 - 11 < f(x) < x2 - 10
(zie voor illustratie hiervan figuur 2).
We kunnen nu 10log(x) vervangen door 1 of gewoon weglaten (vervangen door 0).
We lossen dan op: x2 - 11 = 0 en x2 - 10 = 0.
Dit geeft opvolgend x = 3,31 en x = 3,16
Een benadering van  de wortel zou dus kunnen zijn: x := 3,24.

3. Lineaire interpolatie begin pagina
Ligt een reële oplossing van de vergelijking f(x) = 0 (met f continu) tussen x0 en x1 waarbij f(x0) en f(x1) verschillend teken hebben, dan kunnen we die oplssing als volgt benaderen (zie figuur 3).

figuur 3 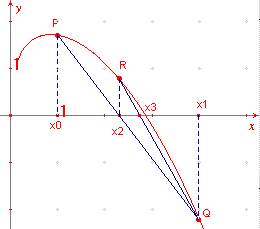benader3 Zij P(x0, y0) en Q(x1, y1), waarbij yi = f(xi), dan snijdt de koorde PQ de x-as in een punt (met x = x2), dat kan worden gebruikt als benadering voor de bedoelde oplossing.
Een betere benadering kan dan worden verkregen door afhankelijk van het teken van f(x2) het proces opnieuw uit te voeren waarbij P of Q vervangen wordt door R(x2, y2).
Enzovoorts.

De vergelijking van de rechte lijn PQ luidt: y - y0 = (y1 - y0)/(x1 - x0) · (x - x0).
Voor y = 0 vinden we hieruit:
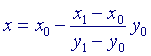
   benader4
zodat
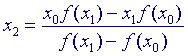
   benader5

Opmerking
We hebben hierbij echter te maken met een langzaam benaderingsproces.
[einde Opmerking]

4. Methode van Newton-Raphson
volgt...

begin pagina

[benader.htm] laatste wijziging op: 30-09-00