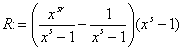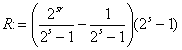Appendix A - Mersenne-priemgetallen
Inleiding | Bewijs ][ Mersenne-priemgetallen
1. Inleiding
We bewijzen hier de in de tekst (Priemgetallen van Mersenne) genoemde
| Stelling ALS 2n - 1 is priem, DAN n is priem |
Voordat we dat doen, zullen we eerst een eenvoudige toelichting geven op de stelling.
We leggen het polynoom P als volgt vast.
> restart: > P := x^(7*3)-1;P := x21 - 1
Het is niet noodzakelijk, dat de ontbinding van de exponent van x uit precies
twee factoren bestaat.
We definiëren vervolgens het polynoom z, met
> z := x^3-1;z := x3 - 1
Nu is P deelbaar door z
> P/z;(x21 - 1) / (x3 - 1)
met als quotient q:
> q := simplify(");
q := x18 + x15 + x12 + x9 + x6 + x3 + 1
We hebben nu dus de volgende ontbinding:
> P = q*z;x21 - 1 = (x18 + x15 + x12 + x9 + x6 + x3 + 1) (x3 - 1)
Algemeen kunnen we nu schrijven:
> P := x^(r*s)-1;P := xrs - 1> z := x^s-1;z := xs - 1> q := Sum(x^(s*i),i=0..r-1);
En dus
> R := value(q*z);
> simplify(");(xs)r - 1
2. Bewijs
We bewijzen de stelling nu via logische omkering.
De beide volgende uitspraken zijn gelijkwaardig:
| ALS 2n - 1 is priem, DAN n is priem - ALS n is niet-priem, dan 2n - 1 is niet-priem |
Bewijs
Stel n is geen priemgetal, dan is n ontbindbaar. Dus n
= r . s, waarbij we zonder de algemeenheid
geweld aan te doen, kunnen stellen, dat 1 < s < n.
We stellen P gelijk aan 2n - 1. En vervolgens substitueren we n =
r . s in deze uitdrukking (zie boven).
Tenslotte kiezen we x = 2 in bovenstaande polynoom-schrijfwijze (P en R), dan is
dus
> subs(x=2, P);2(rs) - 1
En deze uitdrukking heeft een ontbinding (zie boven bij R):
> subs(x=2, R);
We hebben nu bewezen, dat 2n - 1 ontbindbaar is met factor 2s - 1. Dus 2n - 1 is niet-priem. ¨
Gevolg
Omdat x - 1 deelbaar is op xn - 1, moet x - 1 gelijk zijn aan 1,
als xn - 1 een priemgetal is.
Dus hebben we
Zijn a en n natuurlijke getallen. ALS an - 1 is
priem, DAN a = 2 en n is priem
[mersenne_a.htm] laatste wijziging op: 30-11-2002