Passermeetkunde: middelpunt van een cirkel

Mascheroni's constructie | Een tweede constructie  ][  Passermeetkunde

Mascheroni's constructie
Uit: Géométrie du compas, 10e boek / Des centres / 2e druk, Franse editie, pagina 175

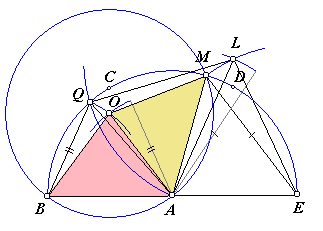Nevenstaande figuur komt overeen met Figuur 71 (plaat 9) uit genoemd boek. De lijnstukken BO, AO, OM em de gekleurde driehoeken zijn echter toegevoegd, ter verduidelijking van het hierna volgende bewijs.

Bewijs:
(We volgen Mascheroni's bewijs, pag. 175-177, in een aangepaste vertaling)
Uit de constructie blijkt dat driehoeken AEL en QAL congruent zijn. Omdat LAB buitenhoek is van AEL hebben we:
LAE = LAQ + QAB = AEL + ALE
waaruit dus volgt dat QAB = ALE = AMQ
En dan vinden we hieruit: LAQ ~ ABQ (immers de tophoeken van deze gelijkbenige driehoeken zijn gelijk).
Nu is LA : AB = AQ : BQ. Vervangen we hierin enkele lijnstukken door hun 'gelijken', dan vinden we: ME : AE = AB : OB.
Hieruit volgt dan: MAE ~ AOB (zzz).
Zodat nu OAB = AME = AEM.
Nu is volgens de stelling van de buitenhoek bij driehoek MAE: MAB = AME + AEM (die aan elkaar gelijk zijn), zodat
MAB = MAO + OAB = 2OAB.
Dus OAB = MAO, waaruit  blijkt dat OAB congruent is met OAM (ZHZ). Dus OA = OB = OM.
En dan is O het middelpunt van de cirkel door A, B en M.

Een tweede constructie
(Floor van Lamoen; juni 2005)

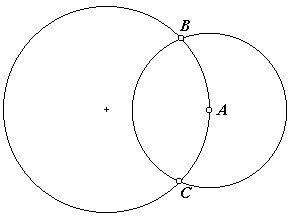	Neem een punt A op de cirkel. Teken een cirkel met middelpunt A die de gegeven cirkel snijdt in B en C. De cirkel moet wel groot genoeg zijn.
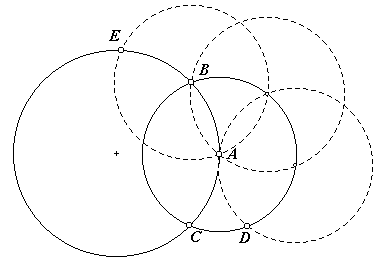	Verdubbel BA naar D met een paar handige cirkels.Het snijpunt van de cirkel met middelpunt B door A, die we voor het verdubbelen van BA nodig hebben, noemen we E.
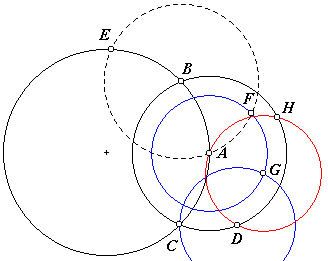	Op dezelfde manier verdubbelen we EB naar F. We tekenen de cirkels met middelpunt D door C en met middelpunt A door F. Noem een van de snijpunten G. Als je eerste cirkel niet groot genoeg was, snijden deze twee cirkels niet. Teken vervolgens de cirkel met middelpunt G door A en D. Deze snijdt de eerst getekende cirkel (met middelpunt A) in D en H.
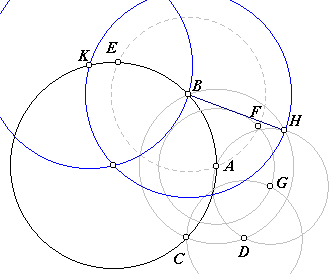	BH is nu gelijk aan de straal van de gegeven cirkel, en de rest is eenvoudig te construeren:

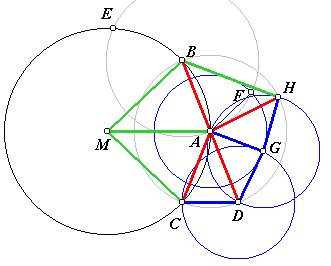Bewijsschets: Als we het middelpunt M noemen, dan is duidelijk dat driehoeken ADC en MBA (en MAC) gelijkvormig zijn, want de tophoek van ADC is gelijk aan die van MBA. Natuurlijk is AF gelijk aan CD en zijn de drie blauwe cirkels dus congruent. Ook zijn driehoeken ADG en AHG congruent (ZZZ), en is driehoek BHA dus aan deze twee gelijkvormig (weer gelijke tophoek). In nevenstaande figuur zijn lijnstukken van gelijke lengte gelijk gekleurd. Uit groen : rood = rood : blauw blijkt nu dat BH inderdaad groen moet zijn.

[passermeetk5.htm] laatste wijziging op: 16-jul-05