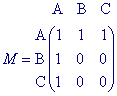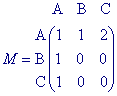Grafen

0. Overzicht

Definities, het Probleem van Königsberg
Verbindingsmatrix, directe-wegenmatrix
Meerstapsverbindingen

1. Definities, het Probleem van Königsberg

Definities
Een graaf is een figuur bestaande uit een eindig aantal punten (knopen) en een eindig aantal verbindingslijnen (takken - tussen die knopen).
Indien voor elk tweetal knopen geldt, dat het aantal takken daartussen ten hoogste 1 is, dan spreken we van een enkelvoudige graaf.
Indien er in een graaf (ten minste) een tweetal knopen verbonden is door meerdere takken, dan spreken we van een meervoudige graaf.
Indien ieder tweetal knopen verbonden is door precies één tak, dan spreken we van een volledige of maximaal verbonden graaf.
Twee knopen die verbonden zijn door ten minste een tak noemen we buren (of verbonden knopen).
Een tak die dezelfde knoop als begin- en eindpunt heeft, heet een lus.

Bovenstaande definitie is zeker niet afkomstig van de Zwitserse wiskundige Leonard Euler (1707-1783). Maar hij was wel de eerste die een grafentheoretisch probleem oploste.
Het probleem
In het 18e eeuwse Königsberg (Koningsbergen) liggend aan de rivier de Oost-Pruisen, tegenwoordig heet het Kaliningrad en de rivier de Pregola, vroegen de bewoners zich af of het mogelijk zou zijn een wandeling te maken over de vier delen van de stad (waaronder Kneiphoff), die verbonden zijn door zeven bruggen, en wel zo, dat iedere brug receis eenmaal werd gebruikt (zie figuur 1, links).
Omdat hun pogingen steeds faalden, geloofden zij, dat een dergelijke wandeling niet mogelijk was.

figuur 1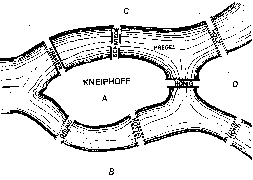

Oplossing:
Euler was de eerst die het probleem oploste (publicatie in 1736, "Solutio problematis ad geometriam situs pertinentis").
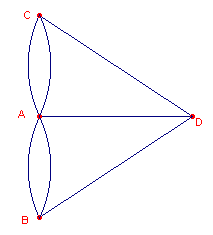
Via abstractie kan het probleem helder worden gemaakt als in figuur 1, rechts.
Indien een punt, niet zijnde het begin of einde van een wandeling wordt bereikt, dan dient dat punt ook weer te worden verlaten. De "valentie" van de punten (valentie=aantal takken van dat punt, aangegeven met de letter v) met uitzondering van ten hoogste 2 punten, moet dus even zijn.
   v(A) = 5
   v(B) = 3
   v(C) = 3
   v(D) = 3
Hieruit volgt dus dat het probleem niet oplosbaar is.
[einde Oplossing]

2. Verbindingsmatrix, directe-wegenmatrix
We kunnen het al of niet verbonden zijn van de knopen in een graaf vastleggen in een matrix (een rechthoekig schema met getallen), verbindingsmatrix.
Ook het aantal wegen tussen de knopen kunnen we in een matrix vastleggen, directe-wegenmatrix.

2.1. Verbindingsmatrix

Definitie
Bestaat een graaf K uit n knopen A₁, A₂, ... A_n, dan heet de bij K behorende nxn-matrix M de verbindingsmatrix van K als
in M geldt
m_ij = 0 als A_i en A_j niet verbonden zijn
m_ij = 1 als A_i verbonden is met A_j (door tenminste 1 tak).

Opmerkingen
[1]
In het algemeen is A_i niet verbonden met zichzelf. Is dit wel het geval, dan is dus m_ii = 1. De tak heet in dit geval een lus.
[2]
Indien A_i wel verbonden is met A_j, maar A_j niet met A_i, dan spreken we van een gerichte tak van A_i naar A_j (de tak bestaat in dit geval uit een lijn met een pijl).
In dit geval is dus m_ij = 1 en m_ji = 0.
[3]
In sommige leerboeken (voor het voortgezet onderwijs) wordt de richting van de verbinding aangegeven "van kolom naar rij" in plaats van "van rij naar kolom" (zoals in bovenstaande definitie en zoals bedoeld is in Opmerking 2.).
[einde Opmerkingen]

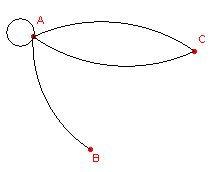
Voorbeeld
We gaan uit van de in figuur 2 staande graaf K. De bijbehorende verbindingsmatrix M staat ernaast. In M zijn, als referentie, de namen van de knopen eveneens opgenomen.

figuur 2

[einde Voorbeeld]

2.2. Directe-wegenmatrix

Definitie
Bestaat een graaf K uit n knopen A₁, A₂, ... A_n, dan heet de bij K behorende nxn-matrix M de directe-wegenmatrix van K als.
in M geldt
m_ij = aantal takken van A_j naar Aj waarbij ook i = j (voor de lussen) is toegestaan.

Voorbeeld
We gaan uit van de in figuur 3 staande graaf K. De bijbehorende directe-wegenmatrix M staat ernaast. In M zijn, als referentie, de namen van de knopen eveneens opgenomen.

figuur 3

[einde Voorbeeld]

3. Meerstapsverbindingen
Via matrixvermenigvuldiging kunnen we het aantal meerstapsverbindingen in een graaf berekenen.

Voorbeeld
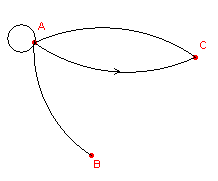
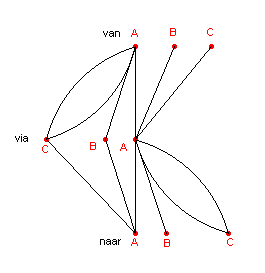
We gaan uit van de graaf in figuur 4a. In figuur 4b staan de takken (die alle moeten worden opgevat als eenrichtingsverbindingen) van A,B,C via A,B,C naar A,B,C.

figuur 4a	figuur 4b

We kunnen nu de matrix M² uit figuur 4b aflezen
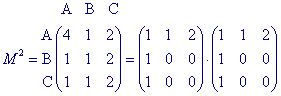
imagesgraf_f1

Stelling
Bij een graaf met n knopen A₁, ..., A_n geeft in de nxn-matrix Mⁿ het element m_ij het aantal n-stapsverbindingen aan tussen A_i en A_j. Hierin is M de directe-wegenmatrix die bij de graaf K behoort.

[grafen.htm] laatste wijziging op: 26-09-1999