Ellips

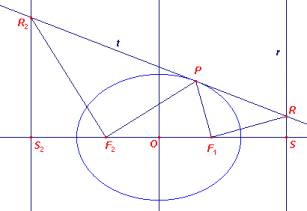
Een meetkundige eigenschap van een ellips

Stelling
De loodlijnen in F₁ en F₂ op de brandpuntsvoerstralen van een punt P van een ellips snijden de raaklijn in P in punten van de richtlijnen.

Bewijs:

richtlijnan_filesimage002

We tonen de stelling aan met behulp van de vergelijking van de ellips (analytisch).

We gaan uit van de ellips met vergelijking:

$\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$

Stel de coördinaten van P zijn: (x₀, y₀).

De raaklijn t in P aan de ellips heeft dan de vergelijking:

$t : \frac{x_{0} x}{a^{2}} + \frac{y_{0} y}{b^{2}} = 1$

We bekijken de situatie voor het brandpunt F₁= (c, 0). Een vergelijking van de bij dat punt behorende richtlijn r is:

$r : x = \frac{a^{2}}{c}$

Voor de coördinaten $(x, y)$ van het snijpunt R van t en r hebben we dan

$R : {\begin{array}{l} x = \frac{a^{2}}{c} \\ \frac{x_{0} x}{a^{2}} + \frac{y_{0} y}{b^{2}} = 1 \end{array}$

Eliminatie van x hieruit levert:

$\frac{x_{0} \frac{a^{2}}{c}}{a^{2}} + \frac{y_{0} y}{b^{2}} = 1 \Rightarrow \frac{x_{0}}{c} + \frac{y_{0}}{b^{2}} y = 1 \Rightarrow y = \frac{b^{2}}{y_{0}} (1 - \frac{x_{0}}{c})$

De coördinaten van R zijn dan:

$R = (\frac{a^{2}}{c}; \frac{b^{2}}{y_{0}} (1 - \frac{x_{0}}{c}))$

We hebben nu als richtingscoëfficiënten rc(F₁R) en rc(F₁P) van de lijnen F₁R en F₁P opvolgend:

$r c (F_{1} R) = \frac{\frac{b^{2}}{y_{0}} (1 - \frac{x_{0}}{c}) - 0}{\frac{a^{2}}{c} - c} = \frac{\frac{b^{2}}{y_{0}} (c - x_{0})}{a^{2} - c^{2}} = \frac{b^{2} (c - x_{0})}{b^{2} y_{0}} = \frac{c - x_{0}}{y_{0}}$

$r c (F_{1} P) = \frac{y_{0} - 0}{x_{0} - c} = \frac{y_{0}}{x_{0} - c}$

Uit beide laatste uitdrukkingen volgt nu eenvoudig:

$r c (F_{1} R) \cdot r c (F_{1} P) = - 1$

waaruit blijkt, dat de lijnen F₁R en F₁P loodrecht op elkaar staan.

[richtlijnan.htm] laatste wijziging op: 30-11-2003