Een eitje, zo'n eitje (ei-vormen)
Constructie | 3:4:5-driehoek | Vijfpunts-ei ][ Meetkunde
Deze pagina is, uiteraard zonder de animaties, als artikel gepubliceerd in Pythagoras, wiskundetijdschrift voor jongeren, december 2000.
Constructie driepunts-ei 
In het oktobernummer (oktober
2000) van het wiskundetijdschrift voor jongeren Pythagoras
beschreef BRUNO ERNST de
constructie van een eivorm met behulp van een aantal
cirkelbogen.
Hieronder is de constructie nog eens weergegeven, samen met de constructiestappen. Alle
constructies kunnen worden uitgevoerd met passer en liniaal.
figuur 1 |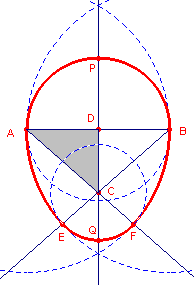
1. Begin met lijnstuk AB met midden D en middelloodlijn van AB. 2. Trek cirkel (D, DA). 3. Kies punt C willekeurig op de middelloodlijn van AB. 4. Trek cirkel (A, AB) en cirkel (B, BA). 5. AC snijdt cirkel A in F, BC snijdt cirkel B in E. 6. Trek cirkel (C, CE). Klik hier |
Een ei-vorm op basis van een 3:4:5-driehoek
Het ei van figuur 1 is opgebouwd uit vier cirkelbogen, waarvan er twee,
AE en BF, congruent zijn. Vanwege de symmetrie kunnen we ook zeggen, dat het ei bestaat
uit drie cirkelbogen en hun spiegelbeeld in de middelloodlijn van AB. De bedoelde
cirkelbogen zijn PA, AE en EQ. De middelpunten van die cirkelbogen zijn opvolgend D, A en
C, die de basisdriehoek van het ei vormen. We hebben een zogenoemd
"driepunts-ei". De verhouding tussen de zijden van die driehoek bepaalt dan de
uiteindelijke vorm van het ei.
figuur 2 |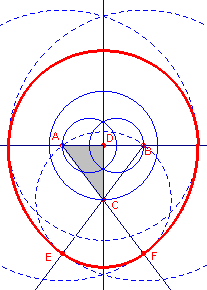
In figuur 2 is een ander driepunts-ei geconstrueerd op
basis van de verhouding 3 : 4 : 5. In de figuur staan ook enkele hulpcirkels waarmee de verhouding tot stand is gekomen. Klik
hier |
figuur 3 |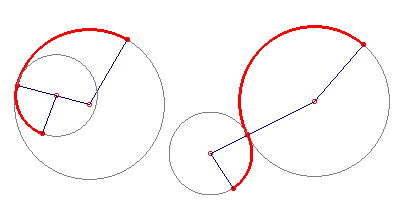
De aansluiting tussen elk tweetal
cirkelbogen moet natuurlijk gladjes verlopen. Dit kan worden bereikt door telkens het
middelpunt van de tweede boog te kiezen op een straal van de eerste cirkel of op het
verlengde ervan. Zie figuur 3. Klik hier |
Vijfpunts-ei
Als je met het bovenstaande rekening houdt, kun je wellicht zelf ook
het in figuur 4 afgebeelde vijfpunts-ei construeren.
figuur 4 |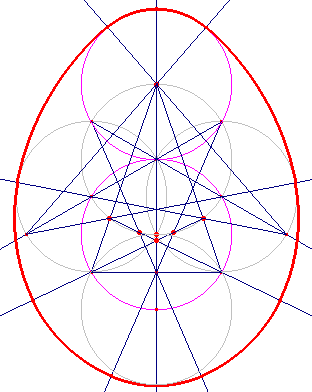
Meer informatie Een boek: ROBERT DIXON, Mathographics, Dover Publications, New York. In dit boek staat ook figuur 4. Internet: |
Naschrift (alleen op deze website)
Klik hier voor een ei-vorm gebaseerd op een regelmatige vijfhoek
[eipyth.htm] laatste wijziging op: 29-08-04