Stelling van Ceva

De stelling van Ceva (iets anders)
We herhalen (zie de pagina "Transversalen"):

Definitie
Onder (ABP), de deelverhouding op de lijn AB bepaald door P, verstaan we: PA/PB (van teken voorzien, dwz. als P op het lijnstuk AB ligt, dan is PA/PB negatief; anders positief).

Stelling van Ceva
Gaan de lijnen AA', BB', CC' in driehoek ABC door één punt P, dan geldt: (ABC')(BCA')(CAB') = -1.

Bewijs:
We tekenen de lijn QR evenwijdig met AB door P.

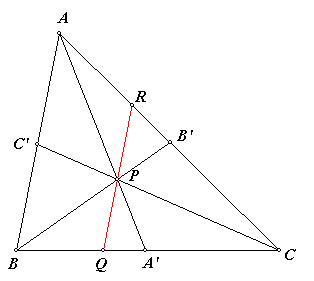Op die evenwijdige lijnen geldt:
(1)...   AC' : C'B = RP : PQ = (RQP)
Verder is in driehoek BA'A':
(2)...   QP : AB =PA' : AA'
en in driehoek BB'A:
(3)...   PR : AB = PB' : BB'
Uit (2) en (3) volgt door deling:
   (QP/AB) : (PR/AB) =(PA'/AA') : (PB'/BB')
zodat
(4)...   PR / PQ = (RQP) = - (PBB') / (PAA')

Uit (1) en (4) volgt dan
(5)... (ABC') = - (PBB') / (PAA')

Zodat ook, analoog aan (5):
(6)... (BCA') = - (PCC') / (PBB') en (CAB') = - (PAA') / (PCC')
Door vermenigvuldiging van (5) en (6) vinden we dan: (ABC')(BCA')(CAB') = -1 ¨

[p: ceva2.htm] laatste wijziging op: 07-02-2005