Gegeneraliseerde stelling van Desargues

Gegeneraliseerde Stelling van Desargues

De Stelling | Gevolgen ][ Stelling van Desargues | Meetkunde

1. De Stelling

Stelling
A1A2A3 (driehoek A) en B1B2B3 (driehoek B) zijn perspectief met punt S als perspector.
(i,j,k) is een permutatie van (1,2,3) ; P_ij = A_iA_k /\ B_jB_k ; C_k = P_ikP_ki /\ P_jkP_kj
Dan is driehoek C1C2C3 (driehoek C) perspectief met driehoek A en met driehoek B, met S als perspector.
(Gegeneraliseerde stelling van Desargues)

Bewijs:

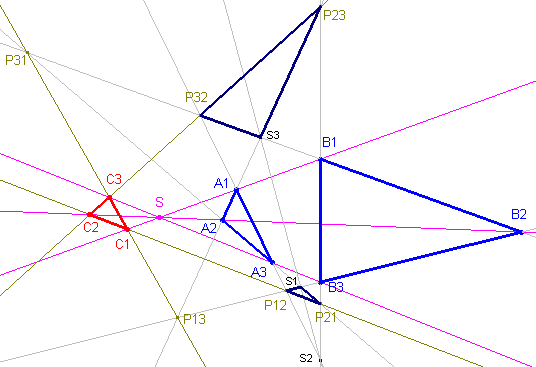Zijn S_k = A_iA_j /\ B_iB_j (i,j,k = 1,2,3).
De punten S_k zijn dan volgens de Stelling van Desargues collineair.
Beschouw nu S1P21P12 en S3P23P32.
Deze driehoeken zijn nu ook perspectief met S2 als perspector, immers:
P21P23 = B1B3, P12P32 = A1A3 en deze lijnen gaan door S2 (enz.).
De snijpunten van de overeenkomstige zijlijnen van deze driehoeken zijn dus collineair (opnieuw volgens Desargues).
A2 = S1P21 /\ S3P23
B2 = S1P12 /\ S3P32
C2 = P21P12 /\ P23P32
Het punt C2 ligt dus op de lijn A2B2.
Evenzo ligt C1 op de lijn A1B1 en C3 op de lijn A3B3.
Dus driehoek C is perspectief met driehoek A en met driehoek B (met het punt S als perspector).
¨

2. Gevolgen
[volgt]

[desargues.htm] laatste wijziging op: 02-10-02