Verdubbelingsformules

Eerste methode

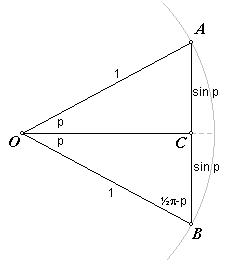In nevenstaande figuur is volgens de sinusregel in driehoek OAB (met OA = OB = 1):
AB / sin2p = OA / sin(½p - p) = 1 / cos p
zodat
2sin p / sin2p = 1 / cos p
en dus

sin 2p = 2sin p · cos p

Volgens de cosinusregel hebben we in die driehoek:
AB² = AO² + BO² - 2·OA·BO·cos2p
of
(2sin p)² = 1 + 1 - 2cos 2p
waaruit volgt

cos 2p = 1 - 2sin²p

Uit deze laatste formule volgt dan eenvoudig, wegens 1 - 2sin²p = 1 - sin²p - sin²p = cos²p - sin²p:

cos 2p = cos²p - sin²p

Tweede methode

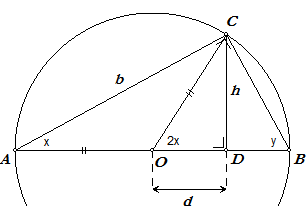We nemen een cirkel met middelpunt O en straal 1 en daarin een 'Thales-driehoek' ABC. CD = h is de hoogtelijn op de schuine zijde.

Volgens de stelling van de omtrekshoek (Euclides, Elementen, Prop. III-20) is nu:
ALS hoek CAB = x, DAN hoek COB = 2x.
In driehoek OCD: sin(2x) = h ...... (1)
In driehoek ACD: sin(x) = h / b, dus h = b · sin(x) ......(2)
In driehoek ABC is y = 90 - x, zodat cos(x) = sin(y) = b / 2, waaruit volgt: b = 2 · cos(x) ......(3)

Uit (1), (2), (3) volgt: sin 2x = 2sin x · cos x

In driehoek OCD is: cos(2x) = d ......(4)
In driehoek ACD is: cos(x) =(d + 1) / b = (d + 1) / (2 · cos x), volgens (3), zodat
d + 1 = 2cos²(x) en dan ook d = 2cos²(x) - 1 ......(5)

Uit (4) en (5) volgt dan: cos 2x = 2cos²x - 1

Derde methode

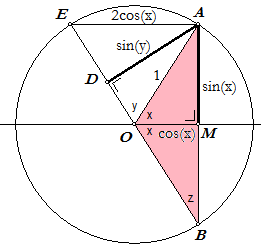In de eenheidscirkel met middelpunt O is getekend driehoek OAB met hoek AOB = 2x.
Nu is in AOM:
AM / AO = sin x, zodat AM = sin x en OM = cos x.

AD is de loodlijn uit A op OB. Dan is: AD = sin y.

We bekijken nu de oppervlakte S van driehoek OAB.
Enerzijds is:
S = 2 · ½ · sin(x) · cos(x) ......(1)
en anderzijds:
S = ½ · AD · OB = ½ · sin(y) = ½ · sin(180 - 2x)= ½ · sin(2x) ......(2)
Uit (1) en (2) volgt dan:
sin 2x = 2sin x · cos x

Verder is:
cos(2x) = cos(180 - y)= - cos(y)
In driehoek AOD = -cos y = - OD = - (1 - DE) = DE - 1......(3)
In driehoek AED is: DE/AE = DE / (2cos(x)) = cos(90-z) = sin z = cos x. Dus:
DE = 2cos²(x) ......(4)
Uit (3) en (4) volgt: cos 2x = 2cos²x - 1

[p: verdub.htm] laatste wijziging op: 05-12-2006