Formules van Simpson

Formule 1 en 2 | Formule 3 en 4 | Download  ][  Analyse

Formule 1:    simpsonf1
Formule 2: simpsonf2
terug

simpson1

Bewijs:
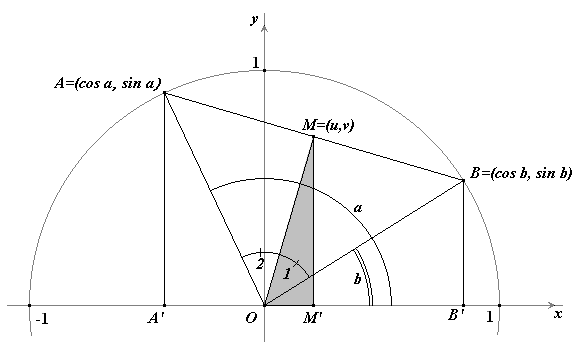
In bovenstaande figuur is M het midden van AB. Zodat:
   v = MM'  =  ½(AA' + BB') = ½(sin a + sin b); eigenschap van de middenparallelel in trapezium A'B'BA.
Verder is in driehoek OM'M:
   O1 = O2 = ½(a - b), en
   MOM'  = ½(a - b) + b = ½(a + b)
   sin½(a + b) = MM' / OM, zodat MM' = OM sin½(a + b)
In driehoek AOM is OM / OA = OM = cos ½(a - b)
Dus:
   v = MM' = sin ½(a + b) cos ½(a - b)
Waaruit formule 1 volgt.

Voor formule 2 hebben we:
   u = OM' = ½(OA' + OB') = ½(cos a + cos b)
en verder:
   u = OM' = OM cos ½(a + b) = cos ½(a + b) cos ½(a - b)
Waaruit formule 2 volgt. ¨

Formule 3:    simpsonf3
Formule 4: simpsonf4
terug
.
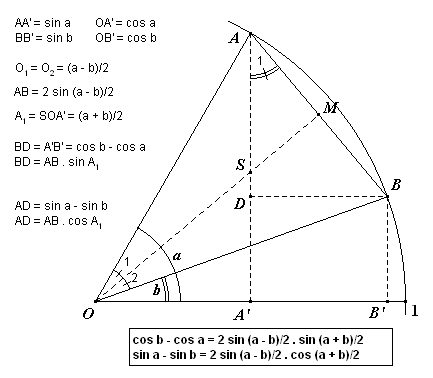
Bewijs:
Vervangen we in formule 1 de variabele b door -b dan volgt daaruit formule 3, wegens sin(-b) = - sin b.
Vervangen we in formule 2 de variabele b door p - b, dan gaat deze over in: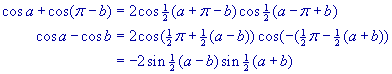
simpsonf5
en we vinden formule 4.¨

Opmerking
De formules zijn genoemd naar Thomas Simpson (1710-1761, Engeland).
De formules worden ook wel goniometrische productformules genoemd, en ook wel p- en q-formules (bij vervanging van a,b door p,q).

In de figuur hiernaast staat een tweede bewijs voor de formules 3 en 4.
[einde Opmerking]

 simpson2

Download terug
De Cabri-figuren op deze pagina kunnen in één bestand worden gedownload (bestemd voor Cabri II en Cabri Plus; zie het ingesloten bestand LEES_DIT.TXT).
Klik hier om het downloadproces te starten (ZIP-bestand; ca. 5 Kb).

begin pagina
[p: simpson.htm] laatste wijziging op: 23-12-2004