Bol, raakvlak, omhullingskegel, omhullingscilinder

Overzicht  ][  Overzicht stereo | Cabri 3D | Meetkunde

Zie ook de pagina "Bol".

Overzicht terug

  1. Inleiding
  2. Raakvlak, omhullingskegel
  3. Omhullend cilindervlak

1. Inleiding terug

figuur 1
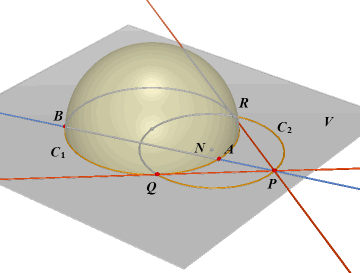bolraak1 Op een bol met middelpunt M liggen de verschillende punten A en B. Op de lijn AB (niet gaande door M) ligt buiten de bol het punt P (zie figuur 1).
Het vlak V door AB en het middelpunt M van de bol snijdt de bol in een grote cirkel C1 (een cirkel waarvan M het middelpunt is).
In V hebben we nu de situatie als in figuur 2.
figuur 2
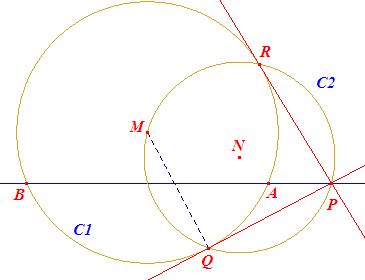bolraak2 De cirkel C2 met middelpunt N (midden van PM) snijdt de cirkel C1 in de punten Q en R.
Nu is MQP = 90º, immers Q ligt op de Thales-cirkel op MP.
En dus: de lijn PQ (en PR) is raaklijn aan de cirkel C1.
  
Definitie
Een lijn door een punt Q op een bol met middelpunt M waarbij MQ loodlrecht staat op die lijn, is een raaklijn aan de bol.

De hiernaast weergegeven situatie geeft aanleiding tot het beschouwen van alle lijnen door Q met MQ loodrecht op die lijn.

We bewijzen nu de hulpstelling:

Stelling 1
Alle loodlijnen in een punt van een lijn loodrecht op die lijn, liggen in een vlak.

Het is voldoende aan te tonen, dat een willekeurige loodlijn ligt in het vlak door twee bepaalde loodlijnen.

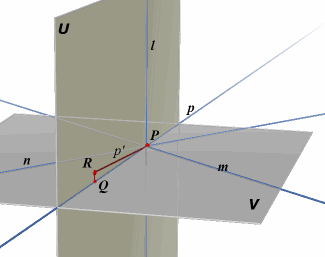bolraak3 Gegeven: m, n, p door P loodrecht op de lijn l.
Te bewijzen: de lijn p ligt in het vlak dat door m en n is aangebracht.

Bewijs:

Stel dat de lijn p niet ligt in het vlak V(m, n).
Zij nu Q een punt van p, en is U het vlak bepaald door Q en l. Dan heeft U het punt P met V gemeenschappelijk.
Er is dus een lijn p' door P die in beide vlakken ligt.
Omdat l loodrecht staat op m, n, staat l loodrecht op V, dus staat l loodrecht op p'.
Gegeven is dat l ook loodrecht staat op p.
In U liggen dus twee lijnen die in p loodrecht op l staan. Dit is evenwel onmogelijk (tegenspraak).
Dus: p ligt eveneens in het vlak V.¨

2. Raakvlak, omhullingskegel terug

Uit stelling 1 volgt nu direct:

Stelling 2
Alle raaklijnen in een punt Q van een bol (met middelpunt M) liggen in hetzelfde vlak, en dat vlak staat loodrecht op de lijn MQ.
Het vlak heet raakvlak in Q aan de bol.

Uit een punt P buiten een bol kan men oneindig veel raaklijnen aan die bol tekenen, immers (zie figuur 1) er zijn oneindig veel vlakken door P en M die de bol snijden, en in elk van die vlakken ligt een cirkel zoals cirkel C1.

Stelling 3
De raaklijnen die uit een punt P buiten een bol (M is middelpunt) aan die bol getrokken kunnen worden, zijn de beschrijvenden van een recht cirkelkegelvlak die P tot top heeft en de de lijn PM als as.
.
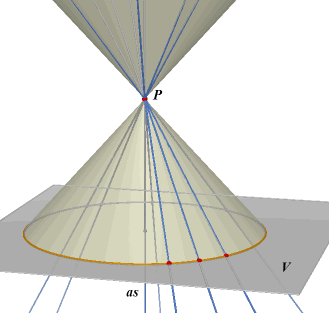bolraak4 Opmerking
Een recht cirkelkegelvlak is de verzameling van alle lijnen die de punten van een cirkel verbinden met een vast punt dat ligt op de loodlijn op het vlak van de cirkel door het middelpunt van de cirkel. De lijnen zijn de beschrijvenden van de kegel, de loodlijn heet de as van het kegelvlak.
[einde Opmerking]

Bewijs (van stelling 3)

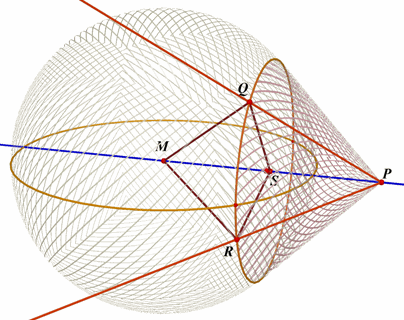bolraak5 PQ en PR zijn raaklijnen aan de bol met middelpunt M. Dus:
MQP = MRP = 90°, MQ = MR, MP MP
De driehoeken MQP en NMRP zijn congruent (ZZR).
Dus MPQ = MPR ......(i)
en PQ = PR ......(ii)
Zij S een punt op PM met QS _|_ MP.
Nu zijn de driehoeken PQS en PRS eveneens congruent (ZHZ), zodat
QS = RS en ook RS _|_ MP.
Het vlak QRS is dus loodvlak op MP. Dit vlak snijdt de bol volgens een cirkel, waarop de punten Q en R gelegen zijn.
PQ en PR zijn dus beschrijvende van een recht cirkelkegelvlak.
Waarmee stelling 3 bewezen is.¨

Men zegt nu dat het kegelvlak de bol omhult. De verzameling raakpunten heet wel de aanrakingskromme.
Het deel van het kegelvlak dat bestaat uit de raaklijnstukken uit het punt P aan de bol (dus lijnstukken als PQ en PR), wordt wel de omhullingskegel (wellicht beter omhullende kegel) van P genoemd.

3. Omhullend cilindervlak terug

Stelling 4
De raaklijnen aan een bol die evenwijdig zijn met een lijn l, zijn de beschrijvenden van een recht cirkelcilindervlak.
.
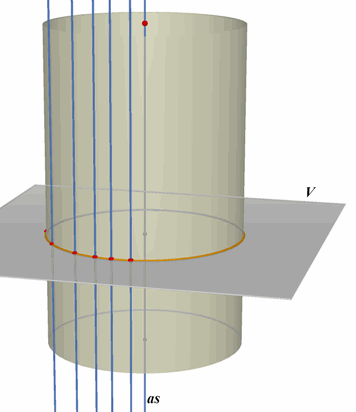cilinder1 Opmerking
Een recht cirkelcilindervlak is de verzameling van alle lijnen die loodrecht staan op het vlak van een cirkel en precies één punt met die cirkel gemeenschappelijk hebben.
De lijnen heten de beschrijvenden van het cilindervlak; de lijn door het middelpunt van cirkel en loodrecht op het vlak van de cirkel heet de as van het cilindervlak.
[einde Opmerking]

Bewijs (van stelling 4):

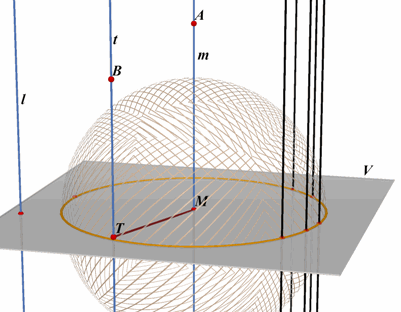cilinder2 Zij l de gegeven lijn. De lijn m = MA is evenwijdig met l en gaat door het middelpunt van de bol.
Als de lijn t = TB de bol raakt in het punt T (met t // l), dan is MTB = 90°.
Daar MA en TB beide evenwijdig zijn met l, is dus ook AMT = 90°.
Het raakpunt T ligt dus op de grote cirkel waarvan het vlak V loodrecht op MA staat.
De lijn t is dus een beschrijvende van het rechte cirkelcilindervlak, dat vastgelegd wordt door de cirkel.
Waarmee stelling 4 bewezen is.¨

Het cilindervlak is een zogenoemd omhullend cilindervlak van de bol.

begin pagina
[p : bol-raakvlak.htm] laatste wijziging op: 01-10-2005