Matrices

Definitie  |  Bewerkingen  |  Eigenschappen  | Determinanten  | Vergelijkingen

---

Wat is een matrix
Een matrix (meervoud: matrices of matrixen) is in principe een eenvoudig wiskundig begrip, dat baseerd is op een eindige rij getallen, zoals de telrij van 3: 3, 6, 9, ..., 30. Zetten we bij telrijen de getallen naast of onder elkaar, bij matrices doen we beide,

Definitie Een matrix is een rij reële getallen die gerangschikt zijn in rijen en kolommen. Om aan te geven dat er sprake is van een matrix worden de tekens [ en ] (of soms ook ( en )) gebruikt (zie figuur 1 en 2). Als m het aantal rijen en n het aantal kolommen is spreekt men van een mxn-matrix of ook van een (m,n)-matrix. Is m = n, dan is er sprake van een vierkante matrix. Het aantal rijen (of kolommen) heet dan de orde van de vierkante matrix. Een kolom van een matrix wordt ook wel kolomvector; een rij van een matrix heet ook wel rijvector. De (p,q)- en de (m,n)-matrix zijn van hetzelfde type (of van dezelfde vorm) als p = m en q = n.

Hebben we bijvoorbeeld 6 getallen, dan kunnen we deze getallen rangschikken als
1 rij met 6 getallen (die 6 getallen vormen dan elk een kolom van de matrix): 1x6-matrix;
2 rijen met 3 getallen: 2x3-matrix
3 rijen met 2 getallen: 3x2-matrix
6 rijen met 1 getal: 6x1-matrix.
Dus (zie figuur 1):

	[1 2 3 4 5 6]		[1 2 3]/ [4 5 6]		[1 2]/ [3 4]/ [5 6]		[1]/ [2]/ [3]/ [4]/ [5]/ [6]
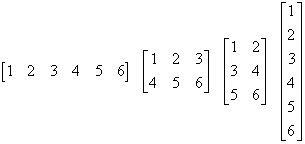figuur 1										figuur 2

NB.
De schrijfwijze van matrices op deze pagina wijkt af van de gebruikelijk notatie voor matrices, omdat ze anders met grafische componenten, als in figuur 2, zouden moeten worden weergegeven
We geven op deze plaats een rij van een matrix dus aan met [ en ] en plaatsen het teken / daarachter, als de matrix op de volgende regel moet worden voortgezet.

De kolom-matrix

[1]/ [2]/ [3]/ [4]/ [5]/ [6]

wordt ook wel aangegeven als

[1 2 3 4 5 6]T.

Voorbeeld
De volgende 3x5-matrix, voorzien van toelichting bij de rijen en kolommen, kan worden gebruikt bij voorraadbeheer. Hierin wordt aangegeven hoeveel stuks van elk artikel op voorraad zijn in een bepaald filiaal van een bedrijf

	Artikel1	Artikel2	Artikel3	Artikel4	Artikel5
Filiaal1:	[5	20	16	7	17       ]/
Filiaal2:	[7	18	12	9	21       ]/	= V
Filiaal3:	[6	25	8	5	13       ]

[einde voorbeeld]

Definitie De (m,n)-matrix [ark] waarvan voor alle r en k geldt ark = 0, wordt aangeduid met O (hoofdletter) en heet nulmatrix. Het feit dat elke nulmatrix wordt aangeduid door O, blijkt geen verwarring te geven.

Bewerkingen met matrices
Gelijkheid van matrices
De matrices A = [a_rk] en B = [b_rk] zijn gelijk (notatie A = B), als ze van hetzelfde type zijn en indien a_rk = b_rk voor r = 1, 2, ..., m en k = 1, 2, ..., n.

Optelling
Twee matrices van dezelfde vorm kunnen worden opgeteld door de elementen in de overeenkomstige rij en kolom bij elkaar op te tellen:

	[a11 a12 ... a1n]/		[b11 b12 ... b1n]/		[a11+b11 a12+b12 ... a1n+b1n]/
A + B =	[a21 a22 ... a2n]/	+	[b21 b22 ... b2n]/	=	[a21+b21 a22+b22 ... a2n+b2n]/
	[ .  ...		[ .  ...		[ .     ...
	[am1 am2 ... amn]		[bm1 bm2 ... bmn]		[am1+bm1 am2+bm2 ... amn+bmn]

We schrijven dit ook wel als
A + B = [a_ij] + [b_ij] = [a_ij+b_ij]
waarbij we dus het formaat van de matrices in het midden laten.

Scalaire vermenigvuldiging
k ^. A = k ^. [a_ij] = [k ^. a_ij]
Bij de scalaire vermenigvuldiging van een matrix met een (reëel) getal k wordt dus elk element van de matrix met k vermenigvuldigd.

Vermenigvuldiging van een rij- en een kolomvector
We definiëren alleen het product van een rijvector en een kolomvector waarvan het aantal elementen aan elkaar gelijk is.

Zij A = [a b c d ]	en B =	[p]/ [q]/ [r]/ [s]
dan is AB = [ap + bq + cr + ds] of ook: AB = [a b c d] [p q r s]T.

Het product van een een rij- en een kolomvector is dus een (1,1)-matrix. Zo'n (1,1)-matrix, [a], wordt ook wel geïdentificeerd met het getal a zelf. Dus
[a] = a.
Het getal a wordt ook wel het inwendig product of inproduct van de beide vectoren genoemd.

Matrixvermenigvuldiging
We definiëren alleen de vermenigvuldiging C = AB van een (m,p)-matrix A met een (p,n)-matrix B; het aantal kolommen in de eerste matrix (A) dient dus gelijk te zijn aan het aantal rijen van de tweede matrix (B).
Dus met de verkorte notatie:
C = AB = [a_ip] ^. [b_pj]=[c_ij], waarbij

cij

=

[ai1 ai2 ... aip]

[b1j]/ [b2j]/ [...]/ [bpj]

=

ai1b1j+a2ib2j+...+aikbpj

Dus: het element c_ij van C is gelijk aan het inproduct van de i-de rijvector van A en de j-de kolomvector van B.

Voorbeelden

[2 -1]/ [0  3]

[ 7  0]/ [-2 -3]

=

[16  3]/ [-6 -9]

[ 3 0 1]/ [-1 2 0]/ [ 0 0 2]

[1  0 0]/ [0 -1 0]/ [1  1 1]

=

[ 4  1 1]/ [-1 -2 0]/ [ 2  2 2]

[3 1 4]/ [2 0 5]

[1 3 0 0]/ [1 1 0 0]/ [0 0 1 1]

=

[4 10 4 4]/ [2  6 5 5]

[einde voorbeelden]

Overige Definities In een matrix A = [ark] noemen we de rij elementen a11, a22, a33, ... de hoofddiagonaal van A. Een vierkante matrix A heet bovendiagonaalmatrix, als alle elementen onder de hoofddiagonaal gelijk zijn aan 0; dwz. voor r > k geldt ark = 0. Een vierkante matrix heet onderdiagonaalmatrix, als alle elementen boven de hoofddigonaal gelijk zijn aan 0 (voor r < k geldt ark = 0). Een diagonaalmatrix is een vierkante matrix D = [drk] met de eigenschap, dat drk = 0 als r ¹ k; alle elementen buiten de hoofddiagonaal zijn dus nul. Een scalaire matrix is een digonaalmatrix D = [drk] waarvoor d11 = d22 = ... = dnn. Is van een scalaire matrix d11 = d22 = ... = dnn = 1, dan noemen we deze matrix een eenheidsmatrix, aangeduid door E. Soms geeft men door een index n de orde van de matrix aan En. Door gebruik te maken van het Kronecker-symbool dij = 1, als i = j 0, als i ¹ j kan men de eenheidsmatrix dus ook aanduiden met E = [dij]. Onder de getransponeerde matrix AT van een gegeven matrix A = [ark] verstaat men de matrx die uit A ontstaat door de rijen met de kolommen te verwisselen; als A = [ark] en AT = [brk], dan is brk = akr; dus (AT)T=A

Eigenschappen
Optelling
De definitie van de optelling van matrices heeft tot gevolg, dat aan de volgende eigenschappen wordt voldaan:

1. A + (B + C) = (A + B) + C
2. A + B = B + A
3. Uit A + C = B + C volgt A = B
4. Voor alle A geldt A + O = A
5. Is A = [a_rk], dan definiëren we -A = [-a_rk] = (-1) . A en dan geldt A + (-A) = 0

Matrixvermenigvuldiging
Voor matrixvermenigvuldiging hebben we (oa.) de volgende eigenschappen.

1. (AB)C = A(BC)
2. A(B + C) = AB + AC
3. (AB)^T = B^TA^T

We geven van deze laatste eigenschap een
Voorbeeld

(

[3 1 4]/ [2 0 5]

[1 3 0 0]/ [1 1 0 0]/ [0 0 1 1]

)T=(

[4 10 4 4]/ [2  6 5 5]

)T =

[4 2]/ 10 6]/ [4 5]/ [4 5]

en

[1 1 0]/ [3 1 0]/ [0 0 1]/ [0 0 1]

[3 2]/ [1 0]/ [4 5]

=

[ 4 2]/ [10 6]/ [ 4 5]/ [ 4 5]

[einde voorbeeld]

4. Als A een (m,n)-matrix is, dan is E_mA = AE_n = A
5. Als A een (m,n)-matrix is, dan is OA = AO = O

Determinanten
We definiëren een functie van de de verzameling der vierkante matrices op de reële getallen. Deze functie noemen we determinant en duiden deze voor de matrix A = [a_rk] aan met det(a_rk) of met det (A) of det A. We gebruiken als notatie:

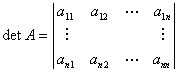
Is de orde van de matrix gelijk aan n, dan noemen we de bijbehorende functie ook een determinant van de orde n.
De berekening van de functiewaarde verloopt op een, op het eerste gezicht, nogal gecompliceerde manier:

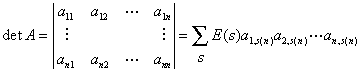
Hierin is s(1), s(2), ..., s(n) een permutatie van de getallen 1, 2, ..., n. Deze sommatie wordt genomen over alle permutaties (de verzameling S). De functie E(s) is gedefinieerd als

E(s) =

+1, als s een even permutatie is - 1, als s een oneven permutatie is

Het aantal termen van de sommatie is dus n!.

Voorbeelden

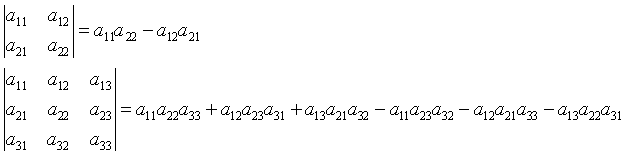
[einde voorbeelden]

Eenvoudig zijn de volgende twee stellingen nu in te zien.

Stelling |a1 + b1  p11 ... p1n|/ |a2 + b2  p21 ... p2n|/ |... |an + bn  pn1 ... pnn| = |a1 p11 ... p1n|/ |a2 p21 ... p2n|/ |... |an pn1 ... pnn|  +  |b1 p11 ... p1n|/ |b2 p21 ... p2n|/ |... |bn pn1 ... pnn|

Bewijs: Dit is gebaseerd op de distributieve eigenschap van de vermenigvuldiging. ¨

Stelling Een determinant wordt met een getal vermenigvuldigd door één van de kolommen (of rijen) met dat getal te vermenigvuldigen.

Bewijs: Dit is eveneens gebaseerd op de distributieve eiegenscahp van de vermenigvuldiging.¨

Stelling Verwisselt men in een (n,n)-matrix twee rijen, dan wisselt de determinant alleen van teken. Verwisselt men in een (n,n)-matrix twee kolommen, dan wisselt de determinant alleen van teken.

Bewijs: Verwisselt men in A = [a_rk] de i-de rij met de k-de rij, dan gaat A over in een andere matrix B = [b_rk], waarin
b_ij = a_kj, b_kj = a_ij met j = 1, 2, ..., n
en
b_hj = a_hj met h ¹ i, h ¹ k, j = 1, 2, ...,n
Nu bevat elke term uit de ontwikkeling van det(A) één element uit de i-de rij en één element uit de k-de rij.
Is nu E(s)a_1,s(1)a_2,s(2)...a_i,j...a_k,l...a_n,s(n)
zo'n term.
Men krijgt dus det(B) uit det(A) door in elke term het element a_ij uit de i-de rij te vervangen door b_ij = a_kj en het element a_kl uit de k-de rij door b_kl=a_il, zodat de genoemde term overgaat in
E(s₁)a_1,s(1)a_2,s(2)...a_k,j...a_i,l...a_n,s(n)
In de oorspronkelijke uitdrukking van det(A) heeft echter de laatste term niet de coëfficiënt E(s), want de permutatie s(1), s(2), ..., k, ...i), ...s(n) ontstaat uit s(1), s(2), ..., i, ..., k, ...s(n) door verwisseling van twee cijfers. Het teken daarvan wijzigt dus.
Op dezelfde manier bewijst men dat det(A) ook van teken verandert, als men in de matrix A twee kolommen verwisselt.¨

Stelling Van een vierkante matrix A met twee gelijke rijen (of kolommen) is det(A) = 0.

Bewijs: Door verwisseling van twee gelijke rijen moet volgens de vorige stelling det(A) van teken wisselen; de matrix zelf verandert daardoor echter niet. Dus det(A) = - det(A).
Dus det(a) = 0. ¨

Ontwikkeling van een determinant naar een rij of een kolom
In elk van de n! termen van de ontwikkeling van det(A) komt een bepaalde rij-index i precies eenmaal voor (en dat zelfde geldt overigens voor een bepaalde kolom-index k).
We nemen nu van alle termen die a_i1 als factor bevatten samen, vervolgens alle termen die a_i2 als factor hebben, enz.
We krijgen nu een verdeling die leidt tot de schrijfwijze

det(A)= a_i11A_i1 + a_i2A_i2 + ...a_inA_in

waarin de factoren A_ik (bestaande uit termen die ontstaan zijn door deling door a_ik) nader moeten worden bepaald.

Stelling Als det(A) = ai1Ai1 + ai2Ai2 + ...ainAin, dan is Aik = (-1)i+k . det(Dik) waarin Dik de matrix voorstelt die uit matrix A ontstaat als men de i-de rij en de k-de kolom daaruit weglaat (dus Dik is een (n-1, n-1)-matrix). Men noemt Dik het algebraisch complement of minor van aik in de matrix A. We schrijven soms M(aik) = Dik

Bewijs: Voor i > 1 verwisselen we de i-de rij achtereenvolgens met de (i-1)-ste, (i-2)-de, ..., 1ste rij (dus i - 1 verwisselingen), en als k > 1 verwisselen we de (k-1)-ste, (k-2)-de, ..., 1-ste kolom (dit geeft k-1 verwisselingen).
Daardoor is det(A) vermenigvuldigd met (-1)^i-1+k-1 = (-1)^i+k; uit de matrix A is daardoor de matrix A' ontstaan met
det(A') = (-1)^i+kdet(A)
Schrapt men in A' de eerste rij en de eerste kolom, dan geldt voor de matrix D'_i1, die zo ontstaat, dat det(D'_i1) = det(D_ik), terwijl de termen van det(A') uit die van det(A) ontstaan door vermenigvuldiging met (-1)^i+k.
Daaruit volgt
A'_il = (-1)^i+kA_ik
waarin A'_il het algebraisch complement is van a'_il = a_ik.
Nu is eenvoudig in te zien, dat A'_il = det(D_ik), dus A_ik = (-1)^i+kdet(D_ik).¨

Men zegt dat de ontwikkeling det(A) = a_i1A_i1 + a_i2A_i2 + ... + a_inA_in de ontwikkeling van det(A) is naar de i-de rij.
Analoog is det(A) = a_1kA_1k + a_2kA_2k + ... + a_nkA_nk de ontwikkeling van det(A) naar de k-de kolom.

Voorbeeld
In beide onderstaande voorbeelden ontwikkelen we de determinaten naar de eerste rij.

1. Zij A =

[a1 b1]/ [a2 b2]

dan is M(a1) = det [b2] en M(b1)= - det [a2], zodat det(A) = a1b2 - b1a2

2. Zij A =

[a1 b1 c1]/ [a2 b2 c2]/ [a3 b3 c3]

dan is

M(a1) =

[b2 c2]/ [b3 c3]

, M(b1) = -

[a2 c2]/ [a3 c3]

en M(c1) =

[a2 b2]/ [a3 b3]

Dus

det(A) =

a1(b2c3-c2b3)-b1(a2c3-c2a3)+c1(a2b3-b2a3).

[einde voorbeeld]

Matrices bij het oplossen van stelsels lineaire vergelijkingen
Door gebruik te maken van de matrix-schrijfwijze van stelsels lineaire vergelijkingen kunnen we deze op eenvoudige wijze oplossen. We zullen hierbij eerst uitgaan van een voorbeeld.
We zoeken de oplossing van het onderstaande stelsel V van vergelijkingen

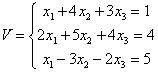
Zoals we gemakkelijk kunnen nagaan is de oplossing van dit stelsel gelijk aan x₁ = 3, x₂ = -2, x₃ = 2.
We schijven nu met behulp van matrix-vermenigvuldiging

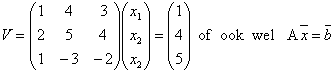
Nu is det(A) = (1)(-10+12)-(4)(-4-4)+(3)(-6-5) = 2 + 32 - 33 = 1.
Voorts beschouwen we de matrices die ontstaan door de kolomvectoren van A te vervangen door de vector b. Deze matrices noemen we opvolgend X₁, X₂ en X₃. Dus:

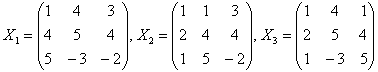
Berekening van opvolgend det(X₁), det(X₂) en det(X₃), steeds via ontwikkeling naar de eerste rij, geeft:
det(X₁) = (1)(2) - (4)(-28) + (3)(-37) = 2 + 112 - 111 = 3;
det(X₂) = (1)(-28) - (1)(-8) + (3)(6) = -28 + 8 + 18 = -2;
det(X₃) = (1)(37) - (4)(6) + (1)(-11) = 37 - 24 - 11 = 2.

We kunnen nu aantonen, dat voor de oplossing van het stelsel V geldt: .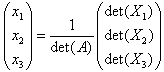
Uit de eerder gegeven oplossing zien we dat dit inderdaad juist is.
We kunnen het bovenstaande algemeen formuleren als:

Stelling Voor het stelsel V van n lineaire vergelijkingen n onbekenden Ax = b, waarbij det(A) ¹ 0, geldt det(A) . xi = det(Xi), waarbij Xi de matrix is die uit de matrix A onstaat door daarin de i-de kolomvector te vervangen door de vector b.

Bewijs: Zij (x₁, x₂, ..., x_n)^T een oplossing van het stelsel. Dan is, blijkens subsitutie in het stelsel, b_j = a_j1x₁ + a_j2x₂ + a_j3x₃ + ... + a_jnx_n (voor j = 1, 2, ..., n), zodat
Nu is 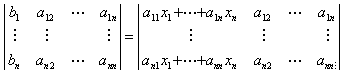. In deze laatste determinant kunnen we de eerste kolom nu verminderen met telkens xi maal de i-de kolom (voor i = 2, 3, ..., n). Daardoor verandert de waarde van de determinant niet. We krijgen zo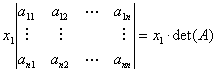
Voor j = 2, 3, ..., n verloopt het bewijs analoog.¨

En tweede methode die gebaseerd is op (alleen de schijfwijze voor) matrices is gebaseerd op de gebruikelijk manier van oplossen van stelsels vergelijkingen.
We schijven daarbij het stelsel op door middel van de zogenoemde aangevulde matrix.
We gebruiken weer het bovenstaande voorbeeld. We krijgen dan opvolgend:

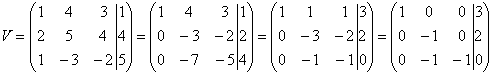
De lezer ga na, dat we in het bovenstaande de volgende bewerkingen hebben uitgevoerd op de rijen van de matrix:

rij2 - 2 keer rij1 rij3 - 1 keer rij1

rij1 plus rij 2    rij3 min 2 keer rij 2

rij1 plus rij3   rij2 min 2 keer rij 3

.

Tenslotte vinden we 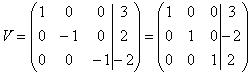met

rij3 min rij2

rij2 keer -1   rij3 keer -1

. Dus: x1 = 3, x2 = -2, x3 = 2.

---

[matrices.htm] laatste wijziging op: 11-05-09 (14-03-2001)